Дипломная работа: Анализ режимов работы электрических сетей ОАО "ММК им. Ильича" и разработка адаптивной системы управления режимами электропотребления

Решение оптимизационной задачи включает в себя следующие этапы:

сбор исходной информации (исходных данных);

составление математической модели, под которой понимается формализованное математическое описание решаемой задачи;

выбор метода решения, определяемого видом математической модели;

выполнение математических вычислений, поручаемое, как правило, компьютеру;

анализ решения задачи.

Математическая модель

Математическая модель – формализованное математическое описание оптимизационной задачи.[1,2] Математическая модель включает в себя:

целевую функцию;

ограничения;

граничные условия.

Целевая функция представляет собой математическую запись критерия оптимальности. При решении оптимизационной задачи ищется экстремум целевой функции, например минимальные затраты или максимальная прибыль. Обобщенная запись целевой функции имеет следующий вид:

(1.1)

где - искомые переменные, значения которых вычисляются в процессе решения задачи;

n - общее количество переменных.

Зависимость между переменными в целевой функции (1.1) может быть линейной или нелинейной.

Ограничения представляют собой различные технические, экономические, экологические условия, учитываемые при решении задачи[1,2]. Ограничения представляют собой зависимости между переменными , задаваемые в форме неравенств или равенств

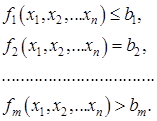(1.2)

Общее количество ограничений равно m.

Граничные условия устанавливают диапазон изменения искомых переменных

(1.3)

где di и Di - соответственно нижняя и верхняя границы диапазона изменения переменной хi.

Методы решения оптимизационных задач

Для решения подавляющего большинства оптимизационных задач используются методы математического программирования, позволяющие найти экстремальное значение целевой функции (1.1) при соотношениях между переменными, устанавливаемых ограничениями (1.2), в диапазоне изменения переменных, определяемом граничными условиями (1.3).

Математическое программирование представляет собой, как правило, многократно повторяющуюся вычислительную процедуру, приводящую к искомому оптимальному решению.[2,3]

Выбор метода математического программирования для решения оптимизационной задачи определяется видом зависимостей в математической модели, характером искомых переменных, категорией исходных данных и количеством критериев оптимальности.

Общая характеристика методов решения задач нелинейного программирования

Когда целевая функция (1.1) и ограничения (1.2) нелинейны и для поиска точки экстремума нельзя или очень сложно использовать аналитические методы решения, тогда для решения задач оптимизации применяются методы нелинейного программирования. Как правило, при решении задач методами нелинейного программирования используются численные методы с применением ЭВМ[3,4,5,6].

В основном методы нелинейного программирования могут быть охарактеризованы как многошаговые методы или методы последующего улучшения исходного решения. В этих задачах обычно заранее нельзя сказать, какое число шагов гарантирует нахождение оптимального значения с заданной степенью точности. Кроме того, в задачах нелинейного программирования выбор величины шага представляет серьезную проблему, от успешного решения которой во многом зависит эффективность применения того или иного метода. Разнообразие методов решения задач нелинейного программирования как раз и объясняется стремлением найти оптимальное решение за наименьшее число шагов.