Дипломная работа: Диплом-Нейросетевая система для управления и диагностики штанговой глубинонасосной установкой
Выход нейрона есть функция его состояния: y = f(s) (2), которая называется активационной. Известны различные виды таких функций, некоторые из которых представлены на рис. 2. Одной из наиболее распространённых является нелинейная функция с насыщением, так называемая сигмоидальная (логистическая) функция:
![]()
При уменьшении a сигмоид становится более пологим, вырождаясь в пределе при a = 0 в горизонтальную линию на уровне 0,5; при увеличении a сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x = 0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмоидной функции — простое выражение для её производной:
![]()
Параллелизм обработки достигается путём объединения большого числа нейронов в слои и соединения определённым образом различных нейронов между собой. В качестве примера простейшей НС приведём трёхнейронный персептрон (рисунок 1.1.-3), нейроны которого имеют активационную функцию в виде единичной пороговой. На n входов поступают некие сигналы, проходящие по синапсам на 3 нейрона, образующие единственный слой этой НС и выдающие три выходных сигнала:
![]()
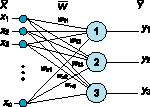
Рисунок 1.1.-3 - Однослойный персепрон
Очевидно, что все весовые коэффициенты синапсов одного слоя нейронов можно свести в матрицу W, в которой каждый элемент wij задаёт величину i-ой синаптической связи j-ого нейрона. Таким образом, процесс, происходящий в НС, может быть записан в матричной форме: Y = F(XW), где X и Y — соответственно, входной и выходной сигнальные векторы, F(V) — активационная функция, применяемая поэлементно к компонентам вектора V. Теоретически число слоёв и нейронов в каждом слое может быть произвольным. Рассматривая классификацию НС, можно выделить: бинарные (цифровые) и аналоговые НС, предварительно обученные (неадаптивные) и самообучающиеся (адаптивные) нейронные сети, что крайне важно при их аппаратной реализации. Бинарные оперируют двоичными сигналами, и выход каждого нейрона может принимать только два значения: 0 либо 1.По топологической классификации НС во внимание принимается число слоёв и связей между ними. На рисунке 1.1.-4 представлен двухслойный персептрон , полученный из однослойного путём добавления второго слоя, состоящего из двух нейронов. При этом нелинейность активационной функции имеет конкретный смысл: если бы она не обладала данным свойством или не входила в алгоритм работы каждого нейрона, результат функционирования любой p-слойной НС с весовыми матрицами W (i) , i = 1,2,...p для каждого слоя i сводился бы к перемножению входного вектора сигналов X на матрицу W (S) = W (1) *W (2) *...*W (p) , то есть фактически такая p-слойная НС эквивалентна однослойной с весовой матрицей единственного слоя W (S) : Y = XW (S) .
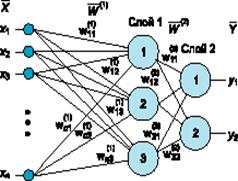
Рисунок 1.1.-4 - Двухслойный персептрон
Одним из самых важных этапов разработки нейровычислителя является обучение нейронной сети. От качества обучения зависит способность сети решать поставленные перед ней задачи. На этапе обучения кроме параметра качества подбора весовых коэффициентов, важную роль играет время обучения. Как правило, эти два параметра связаны обратной зависимостью, и их приходится выбирать на основе компромисса. Обучение НС может вестись с учителем или без него. В первом случае, сети предъявляются значения как входных, так и желательных выходных сигналов, и она по некоторому внутреннему алгоритму подстраивает веса своих синаптических связей. Во втором случае, выходы НС формируются самостоятельно, а веса изменяются по алгоритму, учитывающему только входные и производные от них сигналы.
Существует великое множество различных алгоритмов обучения, которые можно разделить на два больших класса: детерминированные и стохастические. В первом из них подстройка весов представляет собой жёсткую последовательность действий, во втором — производится на основе действий, подчиняющихся некоторому случайному процессу. Практически 80% реализованных на сегодня нейрочипов, ориентированных на задачи цифровой обработки сигналов, используют при обучении НС алгоритм обратного распространения ошибки.
Обучение по алгоритму обратного распространения ошибок.
На протяжении многих лет не знали правила, которое можно было бы использовать для корректировки весов многослойной сети в процессе управляемого обучения. Правило корректировки весов, о котором идет речь, называется алгоритмом обратного распространения ошибок. Алгоритм обратного распространения определяет два потока в сети: прямой поток от входного слоя к выходному и обратный поток — от выходного слоя к входному. Прямой поток продвигает входные векторы через сеть, в результате чего в выходном слое получаются выходные значения сети. Обратный поток подобен прямому, но он продвигает назад по сети значения ошибок, в результате чего определяются величины, в соответствии с которыми следует корректировать весовые коэффициенты в процессе обучения. В обратном потоке значения проходят по взвешенным связям в направлении, обратном направлению прямого потока. Например, в прямом потоке элемент скрытого слоя посылает сигналы каждому элементу выходного слоя, а в обратном потоке элемент скрытого слоя будет получать сигналы ошибок от каждого элемента выходного слоя.
В процессе обучения каждый входной образец будет иметь соответствующий целевой выходной образец, который должен получаться для данного входного.
В общем, целью обучения является нахождение такого набора весовых коэффициентов сети, который обеспечивает решение данной конкретной проблемы. Перед началом обучения весовые коэффициенты устанавливаются равными малым случайным значениям — например, значениям из диапазона от -0.3 до 0.3. Коротко говоря, сети предъявляется образец и вычисляется вектор ошибок, в результате чего выясняется, насколько следует изменить значения весов; процесс повторяется для каждого образца. Полный цикл рассмотрения всех имеющихся образцов называется эпохой. Все образцы подаются на рассмотрение ее снова и снова, эпоха за эпохой, пока на протяжении одной эпохи все значения реального вывода для каждого образца не попадут в допустимые рамки.
1.2.Обзор существующих систем управления ШГНУ
В последние годы созданы вполне работоспособные приборы и целые комплексы, позволяющие регистрировать результаты динамометрирования в электронной памяти этих устройств с последующей (или одновременной) обработкой их на электронно-вычислительных машинах. Программно-математическое обеспечение (ПМО) каждого комплекса имеет свое оформление, требования к исходным данным и используемые методики их обработки.
Рассмотрим системы управления ШГНУ.
Комплексная система исследования работы скважин "Анализатор".
Данная система разработана американской компанией "Есhоmеtег". Она представляет собой комплекс измерительных датчиков. Управление их работой и обработка получаемой информации производятся компьютером совместно с аналого-цифровым преобразователем. Такая система осуществляет обработку данных акустических микрофонов, датчиков давления и нагрузки, акселерометров, датчиков тока двигателя, тахометров и других измерительных устройств.
Для измерения уровня жидкости в кольцевом пространстве скважины акустическим методом эта система используется совместно с генератором импульсов, микрофоном и датчиком давления. Эти измерения используются для определения забойного давления работающей эксплуатационной скважины. А знание пластового давления и использование модели притока жидкости, с учетом определенного анализа, позволяют определять эффективный дебит скважины.
На скважинах со штанговым глубинно-насосным оборудованием данная система применима для динамометрических исследований с измерением нагрузок на полированном штоке, ускорения движения полированного штока и потребляемого двигателем электрического тока. Измерение нагрузок на полированном штоке возможно двумя способами (в зависимости от решаемой задачи).
1. Для количественного динамометрического анализа необходимы данные высокой степени точности, которые можно получить с помощью подковообразного калиброванного датчика, измеряющего механическое напряжение. Он устанавливается между траверсами канатной подвески исследуемой скважины.
2. Для получения качественной информации, позволяющей судить об эффективности работы насоса и выявлять (диагностировать) некоторые неисправности подземного оборудования, используется С-образный облегченный датчик, прикрепляемый при помощи зажима непосредственно к полированному штоку. Датчик замеряет изменение нагрузки на штангах путем замера изменения диаметра полированного штока. Если коэффициент Пуассона для стали равен примерно 0,3, то радиальное напряжение составит около ЗОУ0 от осевой нагрузки.
В обоих случаях для определения перемещения полированного штока используется очень компактный акселерометр на интегральной схеме, который встроен в датчик измерения нагрузки. Таким образом, необходим только один кабель для соединения компьютера и датчика нагрузки. Скорость движения полированного штока является результатом интегрирования сигнала ускорения акселерометра, а повторное интегрирование дает значение положения полированного штока как функции времени. Благодаря высокой скорости обработки информации компьютером, применяемым в комплексе систем "Анализатор", данные динамометрии появляются на экране сразу по мере измерения. В отдельном окне представляется график потребления электрического тока двигателем станка-качалки: анализ потребления электрического тока дает представление об уравновешенности станка-качалки.
Примеры графиков, получаемых при исследовании скважин с помощью комплексной системы "Анализатор", приведены на рисунке 1.2-1
1 — зависимость нагрузки на полированном штоке от положения балансира СКН (несколько циклов);
2 — зависимость нагрузки на полированном штоке от времени;
3 — зависимость нагрузки на полированном штоке от положения балансира СКН;