Дипломная работа: Электромагнитные волны в волноводном тракте

( и —комплексные константы: и ).

Рисунок 1.2

Умножая комплексную амплитуду на и отделяя вещественную часть, находим

(1.10)

Это наложение двух гармонических волн, распространяющихся в противоположных направлениях. Гармоническая волна, движущаяся вдоль оси , возникает как частное решение при.

В качестве другого частного решения рассмотрим наложение бегущих навстречу волн с одинаковыми амплитудами и начальными фазами . При этом из (1.10) получаем

(1.11)

Такой процесс называется стоячей волной. Его отличительной особенностью является синфазность колебаний. Действительно, в каждой области постоянства знака множителя фаза зависит только от времени (это величина или ). В зависимости от косинусоидального изменяется амплитуда гармонических колебаний . Ряд «мгновенных снимков» процесса для разных моментов времени дает картину, показанную на рис. 1.2б; косинусоидальное распределение и вдоль оси не движется (в отличие от бегущей волны), а испытывает «пульсации». При этом расстояния между соседними неподвижными нулями (узлами) равны ; таковы же и расстояния между соседними максимумами (пучностями).

1.3 Поляризация и наложение волн

Для описания ориентации волны, распространяющейся в заданном направлении, существует понятие поляризации. Плоскостью поляризации называют плоскость, проходящую через направление распространения и параллельную вектору . Таким образом, всякое наложение двух волн с произвольными амплитудами и фазами есть также некоторая электромагнитная волна. Любая из плоскостей, проходящих через ось , может в равной мере быть плоскостью поляризации.

Существенно, что при распространении волны плоскость ее поляризации может и не оставаться неподвижной, т. е. волна может изменять свою ориентацию относительно направления распространения. Действительно, рассмотрим электрические поля двух ортогонально поляризованных волн одного направления и составим их наложение

(1.22)

Если фазы волн совпадают ( и ), то, как легко убедиться, наложение волн есть волна, поляризованная в неподвижной плоскости, составляющей угол с плоскостью поляризации первой волны. Это плоская, или линейная, поляризация.

Картина оказывается иной, если фазы налагающихся волн различны. Пусть, например, при одинаковых амплитудах () фазовое различие составляет . Полагая в (1.22) и , определим вектор как

(1.23)

Определяя угол , указывающий положение плоскости поляризации волны, имеем

(1.24)

т. е. угол наклона вектора к оси не остается постоянным в пространстве и времени, а равен . Как видно, в каждой фиксированной плоскости вектор вращается с угловой скоростью , а в фиксированный момент времени распределение поля вдоль оси таково, что конец вектора «скользит по винтовой линии». Это волна круговой поляризации, точнее, левой круговой поляризации. Правая круговая поляризация соответствует случаю и (вращение в противоположном направлении).

Если налагаемые волны имеют произвольные амплитуды и фазы, то результирующий волновой процесс есть волна эллиптической поляризации. Вращаясь, вектор при этом изменяется по величине и описывает эллипс. Ориентация и эксцентриситет эллипса определяются соотношением комплексных чисел и .

Наложение противоположно направленных волн одинаковых амплитуд вызывает процесс, называемый стоячей волной. Особенностью электромагнитной стоячей волны является характерное пространственное и фазовое смещение распределений и .

Рассмотрим, например, стоячую волну, поляризованную в плоскости , Положив и находим

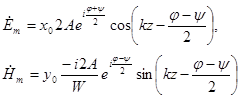(1.25)

или, переходя от комплексных амплитуд к векторам поля в случае идеального диэлектрика (, ):

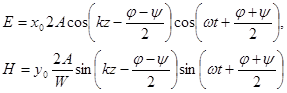(1.26)

Узлы (или пучности) стоячих волн векторов и сдвинуты на четверть волны. Во времени же эти поля смещены на по фазе. Такая стоячая волна в среднем не переносит энергии, как легко убедиться, вычисляя среднюю величину вектора Пойнтинга.

2. Резонансы и направляемые волны в плоских системах

2.1 Плоский резонатор

Распределение поля, возникающее в идеальном диэлектрике при нормальном падении волны на идеально проводящую плоскость, стоячая волна обладает тем свойством, что в любой плоскости, расположенной на расстоянии от границы раздела сред, выполняется условие . Следовательно любую из таких плоскостей можно заменить границей с идеальным проводником, так что в «отсеченном» диэлектрическом слое сможет существовать прежнее поле.