Дипломная работа: Факультативный курс по теме "Элементы комбинаторики" для 8 класса

Перестановки

Два размещения без повторений из n элементов по m состоят из одних и тех же элементов, расположенных в различном порядке. Такие размещения называют перестановками без повторений из n элементов.

где n ! =1∙2∙3∙…∙ n

Читают «n факториал». Считают, что 1!=1, 0!=1. Например, 5!=1∙2∙3∙4∙5=120; 7!=1∙2∙3∙4∙5∙6∙7=5040.

Задача: сколькими способами можно расставить на шахматной доске 8 одинаковых ладей, так, чтобы никакие две из них не били друг друга?

Решение: ладьи не будут бить друг друга тогда и только тогда, когда на каждой горизонтали и каждой вертикали стоит ровно одна ладья. Поэтому будем выставлять их по горизонталям. Первую можно поставить на любые 8 полей первой горизонтали, вторую на 7 полей второй горизонтали (одна вертикаль уже занята первой ладьей) и т.д. Получаем Р₈ =8!=40320 способов.

Пусть дан кортеж длинны п, составленный из элементов множества Х= {х₁ , …, х _k }. Причем элемент х₁ входит в этот кортеж п₁ раз, элемент х _k – п _k раз. Тогда п=п₁ +…+п _k . Если переставлять в этом кортеже буквы, то будут получаться новые кортежи, имеющие тот же состав. Эти кортежи называются перестановками с повторениями из элементов х₁ ,…, х _k , имеющими состав (п₁ , … , п _k ).

Задача: сколько различных кортежей получится, если переставлять буквы слова «математика»?

Решение: это слово имеет состав: м – 2, а – 3, т – 2, е – 1, и – 1, к – 1, то есть (2, 3, 2, 1, 1, 1), поэтому получим Р(2,3,2,1,1,1)=

В размещениях и перестановках важен порядок размещения элементов кортежа.

Сочетания

В отличие от размещений, в сочетаниях порядок элементов множества не важен.

Из элементов множества Х ={7, 4, 5} можно образовывать не только кортежи различной длины, но и различные подмножества, например двухэлементные. В комбинаторике их называют сочетаниями без повторений из трех элементов по два элемента.

Сочетание без повторения из k элементов по m элементов – это m -элементное подмножество множества, содержащего k элементов.

Два сочетания изk элементов поm элементов отличаются друг от друга хотя бы одним элементом.

Число всевозможных сочетаний без повторений из k элементов по m элементов обозначают [23, 154].

Задача: четыре человека сыграли друг с другом по одной партии в шахматы. Сколько было сыграно партий?

Решение: каждую партию можно рассматривать как комбинацию из двух элементов четырех элементного множества, в которой порядок расположения элементов не существен. Но такие комбинации являются сочетаниями без повторений из 4 элементов по 2 и их число равно:

Сочетанием с повторениями из n элементов по k элементов называется всякая последовательность из k элементов, членами которой являются элементы n [29].

=

Задача: сколько наборов из 7 пирожных можно составить, если в продаже имеется 4 сорта пирожных?

Решение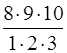: = = = = =120.

В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания [28].

Конечно, применение формул облегчает подсчет числа возможных вариантов решений той или иной комбинаторной задачи. Однако чтобы воспользоваться формулой, необходимо определить вид комбинаций, о которых идет речь в задаче, что бывает сделать не очень просто.

Виды комбинаций		Формула
На «языке» комбинаторики	На теоретико-множественном «языке»
Размещения с повторениями из к элементов по т элементов	Кортежи длины т , составленные из m элементов k -элементного множества (важен порядок элементов).
Размещения без повторений из к элементов по т элементов	Кортежи длиныm , составленные изнеповторяющихся элементов множества, в котором k элементов (важен порядок элементов).
Перестановки с повторениями из n элементов	Кортежи, составленные из n повторяющихся элементов множества (важен порядок элементов)
Перестановки без повторений из к элементов	Размещения из k элементов по k элементов (важен порядок элементов).	Р k = k !
Сочетания без повторений из к элементов по т элементов	m -элементное подмножество множества, содержащего k элементов (порядок элементов не важен)
Сочетания с повторениями из элементов n-типов	Всякая последовательность из k элементов, членами которой являются элементы n (порядок элементов не важен)