Дипломная работа: Геометрии Галилея и Минковского как описания пространства-времени

Слово вектор происходит от латинского глагола vehere – перевозить, перемещать. Английское слово vehicle того же корня обозначает любое перевозочное средство от телеги до космического корабля (space vehicle) [5]. Геометрический вектор указывает прямолинейный переход из одной точки пространства в другую. Из такого представления естественно вытекает определение операции сложения векторов (рис. 1). Если выполнить переход из точки О в точку А, выражаемый вектором , а затем добавить к нему переход из точки А в точку S, выражаемый вектором , то результат двух переходов будет таким же, как прямолинейный переход из точки О в точку S, выражаемый вектором . Поэтому вектор s называют суммой векторов а и b и записывают операцию сложения векторов в виде алгебраического выражения

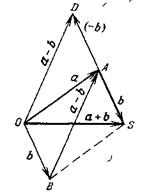
Рис. 1

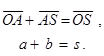(2.1)

Такой способ построения суммы векторов называют правилом треугольника.

Два вектора считаются равными, если посредством параллельного переноса можно совместить точки их начала и конца соответственно. При таком определении равенства векторов становится безразлично, в какой точке приложен вектор (какова точка его начала), и возникает понятие свободного вектора. Свободный вектор не имеет определенной точки начала, и мы имеем право представлять его приложенным в любой точке пространства по своему желанию. Совмещая на рис. 1 начало свободного вектора b с началом вектора а, построим параллелограмм OASB, для которого суммарный вектор является диагональю, исходящей из общего начала складываемых векторов. Такой способ построения суммы векторов называется правилом параллелограмма.

Оба правила (треугольника и параллелограмма) выявляют важное свойство суммарного вектора – он лежит в одной плоскости с векторами-слагаемыми. Пользуясь латинским термином, говорят, что складываемые векторы и суммарный вектор компланарны («соплоскостны»). Для свободных векторов понятие компланарности расширяется: компланарные векторы могут и не лежать в одной плоскости, но существует плоскость, которой параллельны все они и в которую при желании их можно привести посредством параллельного переноса.

Частным случаем перехода из одной точки пространства в другую является отсутствие перехода. Тогда точка конца геометрического вектора совпадает с точкой его начала. Такой вектор называют нулевым и обозначают символом 0. Очевидно соотношение

(2.2)

которое служит алгебраическим определением нулевого вектора.

2.1.2 Псевдоевклидова плоскость

Мир Минковского четырехмерен, но увеличение размерности – не самая главная трудность на пути овладения этим понятием. Гораздо труднее преодолеть барьер необычности метрических свойств пространства Минковского. На первый взгляд они кажутся фантастическими. И если даже математика ручается за их логическую непротиворечивость, остается впечатление, что здесь речь идет о такой математической абстракции, которой нет места в природе. Репутация нереальности метрики мира Минковского тесно связана с сохраняющимся в качестве пережитка представлением о нереальности комплексных чисел, чему сильно способствует и терминология («мнимые» числа). Вот почему необходим небольшой экскурс в эту область.

На протяжении истории науки понятие числа развивалось, приобретая все большую общность. И теперь каждому человеку при получении математического образования приходится в сжатом виде повторять этот процесс расширения понятия числа.

В простейшем представлении число есть количество предметов. Такому представлению соответствует понятие натурального числа (целого положительного). Множество N натуральных чисел замкнуто относительно операций сложения и умножения. Это значит, что, складывая или перемножая любые натуральные числа, мы необходимо будем получать в результате натуральные числа, т.е. не выйдем из множества N.

Операция деления натуральных чисел может привести к дроби, которая не является натуральным числом. Признание дробей числами не вызывало затруднений даже в древние времена. Этот выход за пределы множества N заставил расширить понятие числа. Числом стали называть не только количество предметов, но и отношение количеств.

Несравненно медленнее и труднее формировалось в науке понятие отрицательного числа. Сталкиваясь с необходимостью вычитать из меньшего числа большее, древние математики истолковывали решение как недостаток некоторого количества, но само это количество выражали положительным числом. У них не было числа, которым можно выразить результат такого, например, действия: 2–5 =… И когда они получали при решении уравнения отрицательный корень, то просто отбрасывали его как «недопустимый». «В Европе математики XVI в., хотя и пользовались иногда отрицательными числами, все же называли их «ложными» и «неясными», «меньше, чем ничто» и т.п.» [2]. Лишь в XVII в., после того как Декарт ввел в употребление координатные системы и установил взаимно однозначное соответствие между числами и точками координатной оси, в математике окончательно утвердилось представление о равноправии положительных и отрицательных чисел. Сложилось понятие рационального числа как отношения любых целых чисел т та п. Множество Q рациональных чисел замкнуто относительно операций сложения и вычитания, умножения и деления.

Так потребность в увеличении набора операций, которые можно выполнять над числами, приводила к обобщению понятия числа. Сталкиваясь с задачами, решение которых не могло быть выражено числом в прежнем, узком его понимании, математики приходили к расширению множества объектов, заслуживающих названия числа, формировали новое, более емкое определение числа, включающее в себя и такие числа, которые считались прежде несуществующими или по крайней мере неполноценными. Объективная значимость нового, расширенного понятия числа заключается в том, что с его помощью удается более полно и логически непротиворечиво выражать отношения, существующие в природе.

Точки координатной оси, которым соответствуют рациональные числа, расположены всюду плотно. Это значит, что, сколь бы малый отрезок оси мы ни взяли, на нем найдется бесконечно много точек, служащих образами рациональных чисел. Вместе с тем на любом отрезке координатной оси имеется бесконечно много таких точек, которые не являются образами рациональных чисел. Классическим примером тому, поразившим древних математиков, является задача о сравнении длин стороны квадрата и его диагонали.

Выберем на прямой линии единицу измерения и построим квадрат ОАВС со стороной, равной этой единице. Отложив длину диагонали ОВ на координатной оси, получим отрезок OD (рис. 2). Его длина, очевидно, должна равняться отношению длин отрезков ОB и ОА:

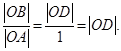
Между тем это отношение отрезков не может быть выражено никаким отношением целых чисел, т.е. никаким рациональным числом. Действительно, по теореме Пифагора имеем

Если допустить, что существуют такие целые числа m и n, отношение которых равно длине отрезка OD, выраженной в единицах :

то придем к противоречию. Мы вправе считать, что числа m и n не имеют общих множителей (при наличии общего множителя можно произвести сокращение на него и в дальнейшем рассматривать уже несократимую дробь). Кроме того, , т.е. не является целым числом, так как из неравенства следует . Возводя равенство в квадрат, мы

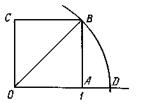
Рис. 2

получили бы . Но числа и не имеют общих множителей, поскольку их не имеют числа и n, причем . Значит, – несократимая дробь, которая не может равняться целому числу 2. Мы доказали, что не существует такого рационального числа, квадрат которого был бы равен 2 [1].

Если считать, что числа могут быть только рациональными, то нельзя выполнять операцию извлечения квадратного корня да числа 2 и символ следует признать лишенным смысла. Он обозначает нечто «потустороннее», не имеющее места в множестве чисел (рациональных чисел). Но такая точка зрения не согласуется с геометрическим содержанием рассмотренной задачи.

Ведь символ в данном случае выражает вполне реальную геометрическую величину – длину диагонали квадрата, сторона которого принята за единицу. Точка D (см. рис. 2), отстоящая на расстоянии этой длины от точки О, реально существует на координатной прямой ОА. Положение этой точки может быть указано приближенно с любой точностью посредством рациональных чисел, которые соответствуют границам сколь угодно малого отрезка, содержащего в себе точку D.