Дипломная работа: Использование балльно-рейтинговой технологии оценивания достижений старшеклассников

5) на основе программных средств организовать учет успеваемости обучающихся и расчет их рейтингов;

6) в конце четверти выставить общую оценку за работу, представляющую собой сумму рейтинговых оценок за отдельные модули [5, с. 38].

Прежде чем представить общую схему организации рейтинговой системы, стоит сказать, что рейтинговая шкала значительно более чувствительна, чем балльная (например, пятибалльная), она представляет собой частный случай ранговой шкалы (см. рис.1). Это позволяет использовать ее для организационных и управленческих решений. Например, в одной из негосударственных школ было принято решение о дифференциации оплаты за обучение детей в зависимости от их успехов, выражаемых рейтингами. В результате одни родители наиболее способных детей были освобождены от оплаты совсем, а родителям детей, создающих наибольшие проблемы и требующих особого усиленного внимания, пришлось доплачивать. В другой негосударственной школе решили ежегодно отчислять 10 учащихся из 300 обучающихся, занимающих нижние строки рейтингового списка, а на их места принимать 10 новичков "с улицы", предоставляя последним счастливый шанс [4, с. 47].

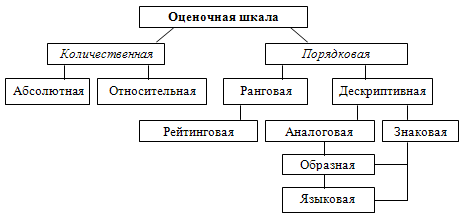
Рис.1 Виды оценочных шкал

Рейтинговая система по ряду признаков имеет большое сходство с количественной шкалой, но, что важно, таковой не является. Рейтинг – это действительное число. Но получается оно либо путем опроса субъективных мнений экспертов, как рейтинги политических деятелей, либо путем набора очков (пунктов, баллов).

Рейтинговая система обладает ни с чем не сравнимой гибкостью. Можно, например, иметь ее отдельно по каждому предмету, а можно общую. В список оцениваемых достижений могут быть включены и неучебные – важные на данный период для статуса или развития школы.

Рассмотрим более детально, как строится рейтинговая система, но сначала необходимо ознакомиться с техникой построения рейтинговых шкал. Пусть требуется ранжировать m объектов E₁ , E₂ , …, E_m и для этого привлечены n экспертов. Это значит, что каждый эксперт должен выдать упорядоченную последовательность данных объектов по степени выраженности оцениваемого свойства, присвоить каждому из объектов ранг от 1 до m. Обозначим r_1к ранг, который присваивает первому объекту k-тый эксперт, r_2к – ранг, который этот же эксперт присваивает второму объекту, и так далее. Например, запись r₂₃ =1 означает, что второму объекту третий эксперт присвоил ранг 1. в результате опроса экспертов получается матрица из m строк и n столбцов (см. таблицу).

Эксперт Объект	1	…	k	…	n
E1	r11	…	r1к	…	r1п
E2	r21	…	r2к	…	r2п
…	…	…	…	…	…
Em	rm1	…	rmк	…	rmп

Но суждения носят оценочный характер и отражают ценностные установки самого эксперта. Здесь велик соблазн для эксперта принять (самому) и представить (другим) свои внутренние критерии в качестве объективных [11, с. 78]. На оценки и суждения экспертов обычно оказывают влияние факторы, которые нельзя отнести к числу научных аргументов: авторитет и заслуги коллег, ранее высказавших суждение; эмоциональная окраска утверждений оппонента и т.п. [20, с. 56]. Поэтому, прежде чем работать с матрицей дальше, следует провести проверку на согласованность экспертных оценок внутри рабочей группы. Для этого найдем суммы R_i по каждой строке:

R_i = r_i1 +…+ r_iк +…+ r_iп

Выберем среди этих сумм наибольшую R_max и наименьшую R_min . Вычислим размах: ΔR=R_max – R_min . Согласованность экспертных оценок считается достаточно высокой, если ΔR= m >. В противном случае требуется более точная и трудоемкая дополнительная проверка по дисперсии. С вероятностью 90% между экспертными оценками имеется достаточная согласованность, если

D>(0,22m+0,50),

где = – среднее арифметическое, а D=– дисперсия.

Формула применима для количества оцениваемых объектов от трех до двадцати.

Если согласованность экспертов достигнута, то дальнейшая процедура проста: объекту с наименьшей суммой рангов присваивается ранг 1, следующему – ранг 2 и т.д. Объект с наименьшей суммой рангов получает итоговый ранг m.

Рассмотрим это в конкретных числах. Предположим, что в конкурсе на оригинальное решение логических задач претендуют на победу 4 ученика: А, Б, В, Г. Жюри из пяти учителей-математик