Дипломная работа: Исследование архитектуры современных микропроцессоров и вычислительных систем
Структура машины II лежит в основе ассоциативных компьютеров (например, центральный процессор машины STARAN), причем фактически такие компьютеры имеют не одно арифметико-логическое устройство, а множество сравнительно простых устройств поразрядной обработки. Другим примером служит матричная система ICL DAP, которая может одновременно обрабатывать по одному разряду из 4096 слов.
Если объединить принципы построения машин I и II, то получим машину III (рис. 1.7). Эта машина имеет два арифметико-логических устройства - горизонтальное и вертикальное, и модифицированную память данных, которая обеспечивает доступ как к словам, так и к битовым слоям. Впервые идею построения таких систем в 1960 году выдвинул У.Шуман , называвший их ортогональными (если память представлять как матрицу слов, то доступ к данным осуществляется в направлении, "ортогональном" традиционному - не по словам (строкам), а по битовым слоям (столбцам)). В принципе, как машину STARAN, так и ICL DAP можно запрограммировать на выполнение функций машины III, но поскольку они не имеют отдельных АЛУ для обработки слов и битовых слоев, отнести их к данному классу нельзя. Полноправными представителями машин класса III являются вычислительные системы семейства OMEN-60 фирмы Sanders Associates, построенные в прямом соответствии с концепцией ортогональной машины.
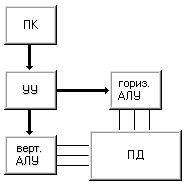
Рисунок 1.7 – Машина III
Если в машине I увеличить число пар арифметико-логическое устройство <=> память данных (иногда эту пару называют процессорным элементом) то получим машину IV (рис. 1.8). Единственное устройство управления выдает команду за командой сразу всем процессорным элементам. С одной стороны, отсутствие соединений между процессорными элементами делает дальнейшее наращивание их числа относительно простым, но с другой, сильно ограничивает применимость машин этого класса. Такую структуру имеет вычислительная система PEPE, объединяющая 288 процессорных элементов.
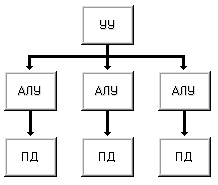
Рисунок 1.8 – Машина IV
Если ввести непосредственные линейные связи между соседними процессорными элементами машины IV, например в виде матричной конфигурации, то получим схему машины V (рис. 1.9). Любой процессорный элемент теперь может обращаться к данным как в своей памяти, так и в памяти непосредственных соседей. Подобная структура характерна, например, для классического матричного компьютера ILLIAC IV.
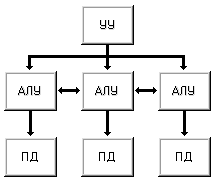
Рисунок 1.9 – Машина V
Заметим, что все машины с I-ой по V-ю придерживаются концепции разделения памяти данных и арифметико-логических устройств, предполагая наличие шины данных или какого-либо коммутирующего элемента между ними. Машина VI (рис. 1.10), названная матрицей с функциональной памятью (или памятью с встроенной логикой), представляет собой другой подход, предусматривающий распределение логики процессора по всему запоминающему устройству. Примерами могут служить как простые ассоциативные запоминающие устройства, так и сложные ассоциативные процессоры.
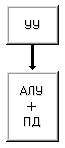
Рисунок 1.10 – Машина VI
1.5 Классификация Хендлера
В основу классификации В.Хендлер закладывает явное описание возможностей параллельной и конвейерной обработки информации вычислительной системой. При этом он намеренно не рассматривает различные способы связи между процессорами и блоками памяти и считает, что коммуникационная сеть может быть нужным образом сконфигурирована и будет способна выдержать предполагаемую нагрузку.
Предложенная классификация базируется на различии между тремя уровнями обработки данных в процессе выполнения программ:
- уровень выполнения программы - опираясь на счетчик команд и некоторые другие регистры, устройство управления (УУ) производит выборку и дешифрацию команд программы;
- уровень выполнения команд - арифметико-логическое устройство компьютера (АЛУ) исполняет команду, выданную ему устройством управления;
- уровень битовой обработки - все элементарные логические схемы процессора (ЭЛС) разбиваются на группы, необходимые для выполнения операций над одним двоичным разрядом.
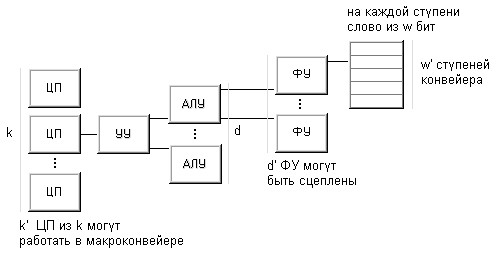
Рисунок 1.11 – Принцип классификации Хендлера
Таким образом, подобная схема выделения уровней предполагает, что вычислительная система включает какое-то число процессоров каждый со своим устройством управления. Каждое устройство управления связано с несколькими арифметико-логическими устройствами, исполняющими одну и ту же операцию в каждый конкретный момент времени. Наконец, каждое АЛУ объединяет несколько элементарных логических схем, ассоциированных с обработкой одного двоичного разряда (число ЭЛС есть ничто иное, как длина машинного слова). Если на какое-то время не рассматривать возможность конвейеризации, то число устройств управления k , число арифметико-логических устройств d в каждом устройстве управления и число элементарных логических схем w в каждом АЛУ составят тройку для описания данной вычислительной системы C:
t(C) = (k, d, w)
Теперь можно расширить возможности описания, допустив возможность конвейерной обработки на каждом из уровней. В самом деле, конвейерность на самом нижнем уровне (т.е. на уровне ЭЛС) это конвейерность функциональных устройств. Если функциональное устройство обрабатывает w-разрядные слова на каждой из w' ступеней конвейера, то для характеристики параллелизма данного уровня естественно рассмотреть произведение w×w'. Знак умножения × будем использовать на каждом уровне чтобы отделить число, представляющее степень параллелизма, от числа ступеней в конвейере. Компьютер TI ASC имеет четыре конвейерных устройства по восемь ступеней в каждом для обработки 64-х разрядных слов, следовательно, он может быть описан так:
t( TI ASC ) = (1,4,64×8)
Следующий уровень конвейерной обработки - это конвейеризация на уровне команд. Предполагается, что в вычислительной системе есть несколько функциональных устройств, которые могут работать одновременно в рамках одного потока команд (в настоящее время используется специальный термин для обозначения данной возможности - сцепление функциональных устройств). Классическим примером этому могут служить компьютеры фирмы CrayResearch. А исторически первой, по всей вероятности, является машина CDC 6600, содержащая десять независимых последовательных функциональных устройств, способных подавать результат своей работы на вход другим функциональным устройствам, образуя единый поток команд:
t(CDC 6600) = (1,1×10,~64)
Наконец, осталось рассмотреть конвейеризацию на самом верхнем уровне, известную как макро-конвейер. Поток данных, проходя через один процессор, поступает на вход другому, возможно через некоторую буферную память. Если независимо работают n процессоров, то в идеальной ситуации при отсутствии конфликтов и полной сбалансированности получаем ускорение в n раз по сравнению с использованием только одного процессора. Так компьютер PEPE, имея фактически три независимых системы из 288-ми устройств, описывается следующим образом:
t( PEPE ) = (1×3,288,32)
После расширения трехуровневой модели параллелизма средствами описания потенциальных возможностей конвейеризации каждая тройка t( PEPE ) = (k×k',d×d',w×w') интерпретируется так: