Дипломная работа: Исследование архитектуры современных микропроцессоров и вычислительных систем

- k' - глубина макроконвейера из отдельных процессоров

- d - число АЛУ в каждом процессоре, работающих параллельно

- d' - число функциональных устройств АЛУ в цепочке

- w - число разрядов в слове, обрабатываемых в АЛУ параллельно

- w' - число ступеней в конвейере функциональных устройств АЛУ

1.6 Классификация Хокни

Р. Хокни - известный английский специалист в области параллельных вычислительных систем, разработал свой подход к классификации, введенной им для систематизации компьютеров, попадающих в класс MIMD по систематике Флинна.

Как отмечалось выше (см. классификацию Флинна), класс MIMD чрезвычайно широк, причем наряду с большим числом компьютеров он объединяет и целое множество различных типов архитектур. Хокни, пытаясь систематизировать архитектуры внутри этого класса, получил иерархическую структуру, представленную на рис. 1.12:

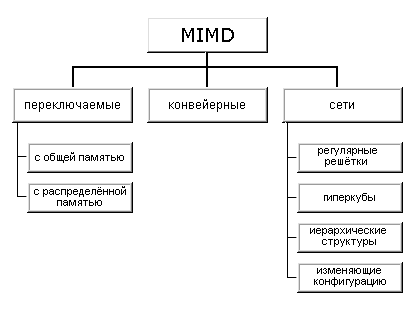
Рисунок 1. 12 – Иерархическая структура класса MIMD

Основная идея классификации состоит в следующем. Множественный поток команд может быть обработан двумя способами: либо одним конвейерным устройством обработки, работающем в режиме разделения времени для отдельных потоков, либо каждый поток обрабатывается своим собственным устройством. Первая возможность используется в MIMD компьютерах, которые автор называет конвейерными (например, процессорные модули в Denelcor HEP). Архитектуры, использующие вторую возможность, в свою очередь опять делятся на два класса:

- MIMD компьютеры, в которых возможна прямая связь каждого процессора с каждым, реализуемая с помощью переключателя;

- MIMD компьютеры, в которых прямая связь каждого процессора возможна только с ближайшими соседями по сети, а взаимодействие удаленных процессоров поддерживается специальной системой маршрутизации через процессоры-посредники.

Далее, среди MIMD машин с переключателем Хокни выделяет те, в которых вся память распределена среди процессоров как их локальная память (например, PASM, PRINGLE). В этом случае общение самих процессоров реализуется с помощью очень сложного переключателя, составляющего значительную часть компьютера. Такие машины носят название MIMD машин с распределенной памятью. Если память это разделяемый ресурс, доступный всем процессорам через переключатель, то такие MIMD являются системами с общей памятью (CRAY X-MP, BBN Butterfly). В соответствии с типом переключателей можно проводить классификацию и далее: простой переключатель, многокаскадный переключатель, общая шина.

Многие современные вычислительные системы имеют как общую разделяемую память, так и распределенную локальную. Такие системы автор рассматривает как гибридные MIMD c переключателем.

При рассмотрении MIMD машин с сетевой структурой считается, что все они имеют распределенную память, а дальнейшая классификация проводится в соответствии с топологией сети: звездообразная сеть (lCAP), регулярные решетки разной размерности (Intel Paragon, CRAY T3D), гиперкубы (NCube, Intel iPCS), сети с иерархической структурой, такой, как деревья, пирамиды, кластеры (Cm^* , CEDAR) и, наконец, сети, изменяющие свою конфигурацию.

Заметим, что если архитектура компьютера спроектирована с использованием нескольких сетей с различной топологией, то, по всей видимости, по аналогии с гибридными MIMD с переключателями, их стоит назвать гибридными сетевыми MIMD, а использующие идеи разных классов - просто гибридными MIMD. Типичным представителем последней группы, в частности, является компьютер Connection Machine 2, имеющим на внешнем уровне топологию гиперкуба, каждый узел которого является кластером процессоров с полной связью.

1.7 Классификация Шнайдера

В 1988 году Л. Шнайдер предложил новый подход к описанию архитектур параллельных вычислительных систем, попадающих в класс SIMD систематики Флинна. Основная идея заключается в выделении этапов выборки и непосредственно исполнения в потоках команд и данных. Именно разделение потоков на адреса и их содержимое позволяет описать такие ранее "неудобные" для классификации архитектуры, как компьютеры с длинным командным словом, систолические массивы и целый ряд других.

Введем необходимые для дальнейшего изложения понятия и обозначения. Назовем потоком ссылок ( reference stream ) S некоторой вычислительной системы конечное множество бесконечных последовательностей пар:

S = { (a₁ t₁ ) (a₂ t₂ )..., (b₁ u₁ ) (b₂ u₂ )..., (c₁ v₁ )(c₂ v₂ )...},

где первый компонент каждой пары - это неотрицательное целое число, называемое адресом, второй компонент - это набор из n неотрицательных целых чисел, называемых значениями, причем n одинаково для всех наборов всех последовательностей. Например, пара (b₂ u₂ ) определяет адрес b₂ и значение u₂ . Если значения рассматривать как команды, то из потока ссылок получим поток команд I; если же значения интерпретировать как данные, то соответствующий поток - это поток данных D.

Интерпретация введенных понятий очень проста. Элементы каждой последовательности это адрес и его содержимое, выбираемое из (или записываемое в) память. Последовательность пар адрес-значение можно рассматривать как историю выполнения команд либо перемещения данных между процессором и памятью компьютера во время выполнения программы. Число инструкций, которое данный компьютер может выполнять одновременно, определяет число последовательностей в потоке команд. Аналогично, число различных данных, которое компьютер может обработать одновременно, определяет число последовательностей в потоке данных.

Пусть S произвольный поток ссылок. Последовательность адресов потока S, обозначаемая S_a , - это последовательность, чей i-й элемент - набор, сформированный из адресов i-х элементов каждой последовательности из S:

S_a = a₁ b₁ ...c₁ ,a₂ b₂ ...c₂ ,...

потока S, обозначаемая S_v , - это последовательность, чей i-й элемент - набор, образованный слиянием наборов значений i-х элементов каждой последовательности из S:

S_v = t₁ u₁ ...v₁ ,t₂ u₂ ...v₂ ,...

Если S_x - последовательность элементов, где каждый элемент - набор из n чисел, то для обозначения "ширины" последовательности будем пользоваться обозначением: w(S_x ) = n.

Из определений S_a , S_v и w сразу следует утверждение: если S - это поток ссылок со значениями из n чисел, то

w(S_a ) = Sи w(S_v ) = nS,

где S обозначает мощность множества S.