Дипломная работа: Исследование методов разнесенного приема в декаметровом канале связи

Пространственный коэффициент корреляции для KB радиолиния довольно точно аппроксимируется зависимостью

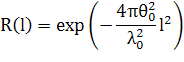
где - средние квадрат телесного угла, под которым виден рассеивающий объем.

1.2. Прием с оптимальным линейным сложением

Рассмотрим принципы построения систем с оптимальным линейным сложением, которые являются основой не только при изучении систем разнесенного приема, но и при построении систем с накоплением (сверткой) сложных сигналов в случае, когда замирания достаточно быстрые и элементарные сигналы оказываются слабо коррелированными.

Запишем равенство в виде

(1)

Так как составляющие шума можно полагать случайными некоррелированными величинами, имеющими нулевые средние значения, а среднеквадратичное значение составляющих сигнала

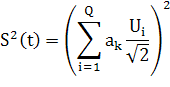
где ; - амплитуда составляющей сигнала в i-й ветви, то отношение средних квадратов сигнала и шума можно записать в виде

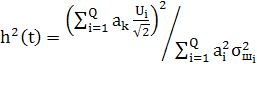(2)

Соотношение (3) можно выразить через величины , характеризующие отношение сигнал/шум в каждой ветви разнесения

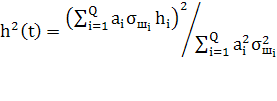(3)

так как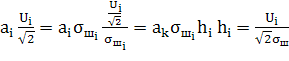

В соответствии с неравенством Буняковского-Шварца числитель дроби (3) можно записать как

(4)

Подставив (4) в (3) и произведя простейшие преобразования, получим

(5)

Этот результат показывает, что максимально возможное значение отношение мощностей сигнала к шуму, получаемое при оптимальном линейном сложении, равняется сумме отношений сигнал/шум по мощности на выходах всех ветвей разнесения.

Пусть теперь

(6)

где - некоторый коэффициент пропорциональности, не зависящий от i ;

Тогда после подстановки (6) в (2) получим

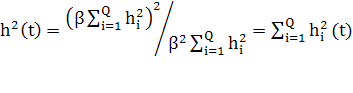(7)

Из (7) следует, что если брать взвешивающие коэффициенты в соответствии с (6), а именно

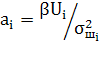(8)

то отношение сигнал/шум может достигнуть максимально возможного значения, равного сумме отношений сигнал/шум в ветвях разнесения.

Следовательно, при оптимальном линейном сложении в любой интервал времени меньший интервала автокорреляции сигнала , взвешивающий коэффициент автоматически должен регулироваться так, чтобы он был прямо пропорционален корню квадратному из среднеквадратического значения сигнала в i-й ветви разнесения и обратно пропорционален среднеквадратическому значению шума в той же ветви. При этом коэффициент пропорциональности выбирается одинаковым для всех ветвей разнесения.

Найдем теперь закон распределения случайной величины , являющейся в соответствии с (7) суммой случайных величин .