Дипломная работа: Исследование особенностей граничного трения ротационным вискозиметром

Для определения объема жидкости, протекающей через щелевой зазор, использовалась (рис.2) калиброванная измерительная трубка 1, высота столба жидкости в которой фиксировалась катетометром К с точностью 0,01 мм. Для создания перепада давлений вискозиметр через балластную трубку 2 подсоединялся к ресиверу 3 с манометрическим устройством 4. При измерении давлений P ~ 10² ¸ 10⁴ Па использовался водяной, а для больших давлений (до 20 КП) – образцовый механический манометр. Для уменьшения объема пленки жидкости, остающейся за опускающимся мениском, диаметры измерительной трубки выбирались небольшими (~ 1 мм). Поверхности пластин, образующих зазор, и другие металлические детали, входящие в контакт с исследуемой жидкостью, перед сборкой вискозиметра для очистки от органических загрязнений промывались растворителем и просушивались.

После установки заданной величины зазора D он герметизировался. Изотермичность и малость градиентов температур ( DT/l £50 K/м) контролировались системой термопар, а постоянство температуры ( DТ £ 0,5 К) в рабочей ячейке обеспечивалось воздушным термостатом. Для устранения ошибки, связанной с возможным шунтированием потока жидкости, ее протечкой через неплотности резиновых прокладок, предварительно проводился контрольный опыт, при котором через вискозиметр прокачивался воздух и определялась объемная скорость его протекания. Рассчитанные в таких опытах значения вязкости воздуха сравнивались с табличными данными, и в дальнейших измерениях вводилась соответствующая поправка. При зазорах D ³ 50 мкм поправка не превышала нескольких процентов, а при меньших зазорах становилась значительной.

После заполнения вискозиметра исследуемой жидкостью в ресивере создавалось разрежение, и при различных фиксированных перепадах давлений DP в диапазоне DP = 10² ¸ 10⁴ Па проводились измерения интервала времени t протекания через прибор заданного объема жидкости Q . Разброс отсчетов времени в пределах серии измерений был ~ 1%, однако, воспроизводимость последовательных серий достигала 10%, что связано, по-видимому, с возможным попаданием в зазор отдельных частиц твердых примесей. Расход жидкости в единицу времени определял экспериментальную объемную скорость течения q_э = Q/ t (м³ /с), где Q – объем протекшей через капиллярный зазор жидкости за время t, и среднюю (по сечению зазора S) линейную скорость <v_э > = q_э /S . Режимы течения во всех проведенных опытах были ламинарными (Re £ 1). «Объемная» вязкость исследовавшихся жидкостей измерялась стандартными вискозиметрами и сравнивалась с литературными данными.

1.2.2 Экспериментальные результаты. В работе авторами были проведены измерения вязкости тонких (D = 30 ¸ 50 мкм) прослоек индивидуальных органических жидкостей и углеводородных технических смесей, образованных между металлическими пластинами. В случае ламинарного потока средняя скорость <v_п > течения ньютоновской жидкости через щелевой зазор толщиной D (рис.3) определяется формулой:

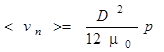, (2.1)

где p= DP/l (Па/м) – градиент давления по длине зазора l , а m₀ (Па·с) – величина коэффициента вязкости жидкости.

Существование на боковых поверхностях щелевого зазора пристенного слоя с иными реологическими характеристиками, чем объемная жидкость, было установлено в опытах с описанным вискозиметром при анализе характера возрастания скорости течения жидкости <v_э > с повышением перепада давления, и сравнением таких зависимостей с теоретическими, рассчитываемыми по (1). Для исследуемых жидкостей при зазорах заведомо больших чем 2d_s , т.е. в отсутствие перекрытия пристенных слоев, в области малых перепадов давления наблюдается уменьшение вязкости с ростом давления и поэтому нелинейное возрастание скорости течения жидкости, а при давлениях (0.5 ¸ 1) 10⁴ Па вязкость становится равной вязкости объемной жидкости.

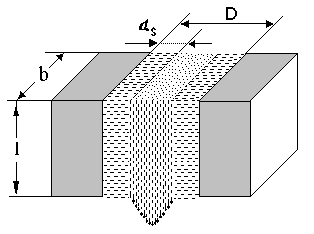???.3. ????????? ???????? ?????? ???????????? ? ????? ??????? ? ??? ???????? ? ???????????????? ????????? ?????

Как пример авторы приведят результаты (рис.4) опытов с технической углеводородной жидкостью МРХ-30. Для тонких (D ~ 30 ¸ 40 мкм) прослоек этого масла при

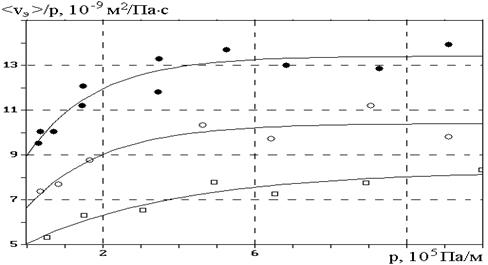
Рис.4. Зависимость отношения <v_э >/ p – относительной (по отношению к градиенту давления p) экспериментальной средней скорости течения масла МРХ-30 через щелевые зазоры вискозиметра от градиента давления p . Величина зазоров: D₁ = 39,7 мкм (·), D₂ = 35 мкм (О) и D₃ = 30 мкм ( ). Т = 294 К. Сплошные линии – аппроксимация зависимостью (2)

небольшой скорости течения зависимость (1) не выполняется – величина <v_э > возрастает не пропорционально градиенту давления p . Экспериментальные результаты трех серий вискозиметрических опытов (при температуре Т = 294 К) с истечением этой жидкости через зазоры трех фиксированных толщин (D ₁ = 39,7 мкм, D ₂ = 35 мкм и D ₃ = 30 мкм) представлены на рис.4 в виде зависимости относительной (по отношению к градиенту давления p ) скорости течения – величины (<v_э >/p , м² /Па×с) от p . Экспериментальные данные аппроксимированы (сплошная линия) функцией:

, (2)

где u _¥ , u₀ и p _¥ – параметры аппроксимирующей зависимости (приведены в табл.1).

Таблица.1

Параметры аппроксимации (2) экспериментальной зависимости относительной (по отношению к градиенту давления p ) средней скорости <v_э >/p = f( p) течения масла МРХ-30 от градиента давления p в щелевых зазорах вискозиметра трех фиксированных толщин D . Т = 294 К.

Толщина зазора D, мкм	Параметры аппроксимации
	u¥,×10–9, м2/Па×с	u0 ×10–9, м2/Па×с	p¥×105, Па/м
39,7	13,4	4,41	1,81
35	10,4	3,74	2,02
31	8,3	3,24	4,04

Из рис.4 видно, что в области малых градиентов давления p < 0,5 МПа/м величина отношения <v_э >/p с увеличением давления растет и лишь при градиентах ( p > 0,5 МПа/м) c повышением давления практически не изменяется. При этом экспериментальная скорость истечения жидкости <v_э > меньше расчетной <v_п > , а при больших перепадах давления становится равной ей.

1.2.3 Обсуждение результатов и модель «жесткого, срезаемого» пристенного слоя.

Наблюдаемый характер зависимости <v_э >/p = f(p) объясняется существованием в прослойке пристенных слоев толщиной 2d_s . Их наличие приводит к тому, что реальное проходное сечение зазора s , по которому протекает жидкость, меньше, чем геометрическое S=bD (рис.3). С ростом приложенного давления и соответственно скорости течения равновесная толщина слоя на каждой из подложек уменьшается и, начиная с какого–то значительного перепада давления, проходное сечение зазора совпадает с геометрическим.

Поэтому для расчета параметров слоя рассмотрим его простейшую реологическую модель: на поверхностях обеих пластин, ограничивающих зазор, существует неподвижный (гидродинамически «жесткий») слой, периферийная часть которого “срезается” течением (рис.3). При постепенном увеличении скорости течения (за счет повышения перепада давления D P ) толщина пристенного слоя убывает вплоть до нуля.

В такой модели, в соответствии с (1), рассматриваемая величина отношения <v_э >/p может быть представлена в виде: