Дипломная работа: Математическое моделирование пластической деформации кристаллов
Удобно при этом выбрать в качестве единицы длины ![]() , единицы энергии
, единицы энергии ![]() и единицы массы - массу атомов
и единицы массы - массу атомов ![]() (полагаем, что материал состоит из атомов одного сорта). Это приводит к ускорению вычислений. Чтобы перейти к величинам, характеризующим конкретный материал, необходимо ввести соответствующие масштабные множители -
(полагаем, что материал состоит из атомов одного сорта). Это приводит к ускорению вычислений. Чтобы перейти к величинам, характеризующим конкретный материал, необходимо ввести соответствующие масштабные множители - ![]() для длины,
для длины, ![]() для времени,
для времени, ![]() для скорости,
для скорости, ![]() для силы,
для силы, ![]() (
(![]() в двумерном случае) для напряжения, где
в двумерном случае) для напряжения, где ![]() и
и ![]() взяты для данного материала.
взяты для данного материала.
Потенциал Леннарда-Джонса простирается до бесконечности. Однако на больших расстояниях он мал. И поэтому его влияние на движение далеких атомов мало. Чтобы ускорить вычисления эту несущественную часть потенциала отбрасывают, или, другими словами, вводят обрезание потенциала
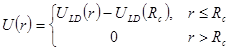 . . | (3) |
Радиус обрезания ![]() традиционно выбирают
традиционно выбирают ![]() или
или ![]() . Возможные причины такого выбора будут обсуждаться ниже. В данной работе будет использоваться радиус обрезания
. Возможные причины такого выбора будут обсуждаться ниже. В данной работе будет использоваться радиус обрезания ![]() . Другие необходимые изменения в потенциале Леннарда-Джонса будут обсуждаться в разделе, посвященном выполнению закона сохранения энергии в МД.
. Другие необходимые изменения в потенциале Леннарда-Джонса будут обсуждаться в разделе, посвященном выполнению закона сохранения энергии в МД.
1.3. Алгоритм интегрирования по времени
Основным компонентом программ, использующих метод молекулярной динамики, является алгоритм интегрирования по времени. Он необходим, чтобы проинтегрировать уравнения движения взаимодействующих частиц и найти их траектории.
Алгоритм интегрирования по времени основывается на методе конечных разностей, время при этом задается на конечной сетке, шаг по времени есть расстояние между последовательными точками сетки. Зная положения и скорости в момент времени ![]() (точные детали зависят от типа алгоритма) схема интегрирования дает те же величины в более поздний момент времени
(точные детали зависят от типа алгоритма) схема интегрирования дает те же величины в более поздний момент времени ![]() . Используя процедуру интегрирования временную эволюцию системы можно прослеживать в течении длительного времени.
. Используя процедуру интегрирования временную эволюцию системы можно прослеживать в течении длительного времени.
Конечно, эти схемы приближенными, и, поэтому, существуют ошибки, связанные с ними. Они классифицируются так:
Ошибки обрывания, связанные с точностью метода конечных разностей по отношению к истинному решению. Метод конечных разностей обычно базируется на ряде Тейлора, оборванном на некотором члене. Эти ошибки не зависят от программной реализации метода, они присущи самому алгоритму.
Ошибки округления, связаны с ошибками, возникающими при программной реализации алгоритма. Например, такие ошибки возникают из-за конечного числа цифр, используемых в компьютерной арифметике.
Оба типа ошибок можно уменьшить, уменьшая ![]() . Для больших
. Для больших ![]() ошибки обрывания доминируют, но они быстро уменьшаются, когда
ошибки обрывания доминируют, но они быстро уменьшаются, когда ![]() уменьшается. Например, алгоритм Верле имеет ошибки обрывания пропорциональные
уменьшается. Например, алгоритм Верле имеет ошибки обрывания пропорциональные ![]() для каждого временного шага интегрирования. Ошибки округления падают более медленно с уменьшением
для каждого временного шага интегрирования. Ошибки округления падают более медленно с уменьшением ![]() и доминируют в пределе малых
и доминируют в пределе малых ![]() . Использование 64-битной точности (соответствующую “двойной точности” в Fortrane) помогает сохранить ошибки округления минимальными.
. Использование 64-битной точности (соответствующую “двойной точности” в Fortrane) помогает сохранить ошибки округления минимальными.
В молекулярной динамике наиболее часто используемым алгоритмом интегрирования по времени является, вероятно, так называемый алгоритм Верле [5]. Основная идея состоит в том, чтобы записать разложение Тейлора до третьего порядка вперед и назад по времени. Пусть ![]() обозначает скорость,
обозначает скорость, ![]() - ускорение и
- ускорение и ![]() - третью производную от
- третью производную от ![]() по
по ![]() . Тогда имеем:
. Тогда имеем:
| (4) |
Складывая эти 2 выражения получаем
| (5) |
Это основная формула алгоритма Верле. Так как мы интегрируем уравнения Ньютона, то ![]() есть просто сила, деленная на массу, и сила в свою очередь есть функция положения
есть просто сила, деленная на массу, и сила в свою очередь есть функция положения ![]() :
:
| (6) |
Видно, что ошибка обрывания алгоритма, когда система эволюционирует в течении времени ![]() , есть величина порядка
, есть величина порядка ![]() , даже если третья производная не появляется в явном виде. Этот алгоритм в тоже время является простым для программной реализации, точным и стабильным, что объясняет его большую популярность при МД моделировании.
, даже если третья производная не появляется в явном виде. Этот алгоритм в тоже время является простым для программной реализации, точным и стабильным, что объясняет его большую популярность при МД моделировании.
Проблема с этой версией алгоритма Верле состоит в том, что скорости явно не вычисляются. Хотя они не нужны для временной эволюции, но их знание иногда необходимо. Кроме того, они нужны для вычисления кинетической энергии ![]() , чья оценка необходима чтобы проверить сохранение полной энергии
, чья оценка необходима чтобы проверить сохранение полной энергии ![]() . Это один из наиболее важных тестов, указывающих, что МД моделирование выполняется корректно. Можно вычислить скорости из положений использую формулу
. Это один из наиболее важных тестов, указывающих, что МД моделирование выполняется корректно. Можно вычислить скорости из положений использую формулу
| (7) |
Однако, ошибки, которые дает это выражение, порядка ![]() а не
а не ![]() .
.
Чтобы преодолеть эту трудность, были развиты варианты алгоритма Верле. Они дают точно ту же траекторию и отличаются переменными, которые хранятся в памяти. Leap-frog алгоритм есть один из таких вариантов.
Лучший реализацией того же основного алгоритма есть так называемый алгоритм Верле со скоростью, когда положение скорости и ускорения в момент времени ![]() получается из тех же величин в момент времени
получается из тех же величин в момент времени ![]() следующим образом:
следующим образом:
| (8) |
Заметим, что необходимо 9N ячеек памяти, чтобы сохранить 3N положений, скоростей и ускорений, но нам не нужно одновременно хранить значения любой из этих величин для двух различных времен.
1.4. Процедура минимизации
Чтобы моделировать деформацию при нулевой температуре используется процедура минимизации, которая позволяет поддерживать систему вблизи локального минимума энергии все время. Деформация и минимизация выполняются одновременно. Алгоритм минимизации представляет собой модифицированный алгоритм МД. После каждого шага по времени МД для каждого атома вычисляется скалярное произведение между импульсом и силой. Для атомов, скалярное произведение для которых отрицательно, импульс зануляется, так как эти атомы движутся в направлении, в котором потенциальная энергия возрастает. Таким образом, кинетическая энергия атомов удаляется, тогда как потенциальная энергия приближается к локальному минимуму энергии вдоль направления движения атома. Такая процедура минимизации быстро сдвигает систему в окрестность локального минимума энергии, но полной сходимости не получается, так как полная сходимость требует числа шагов по времени порядка числа степеней свободы системы. Однако, обычно увеличении числа шагов процедуры минимизации приводит лишь к малым изменениям в эволюции системы.
1.5. Вычисление сил
Наибольших вычислительных усилий требует вычисление сил, действующих между атомами. Поэтому оптимизации алгоритма вычисления сил необходимо уделить особое внимание. Один из шагов в этом направлении состоит в замене сложных для вычисления выражений для сил (например, содержащих экспоненту) на легко вычисляемые выражения (например, сплайны третьего порядка). Второй шаг состоит в использовании потенциалов с ограниченным радиусом действия, или, как указывалось выше, в обрезании несущественной области потенциала, если радиус действия потенциала бесконечен. При этом необходимо вычислить только силы, действующие со стороны ближайших атомов, т.е. находящихся внутри сферы (окружности в двумерном случае) с радиусом равным радиусу обрезания ![]() .
.
Третий шаг состоит в оптимизации алгоритма поиска атомов, ближайших к данному атому. Дело в том, что прямолинейный перебор всех атомов, вычисление расстояний до них и отбрасывание тех атомов, расстояние до которых превышает радиус обрезания ![]() , требует количества операций пропорционального
, требует количества операций пропорционального ![]() , где
, где ![]() - число атомов в системе. Следовательно, с ростом
- число атомов в системе. Следовательно, с ростом ![]() число требуемых операций быстро возрастает, и поэтому выполнение вычислений сильно замедляется, а, для больших
число требуемых операций быстро возрастает, и поэтому выполнение вычислений сильно замедляется, а, для больших ![]() , делается практически невыполнимым. Таким образом, чтобы избежать этого замедления нужен алгоритм, для которого число требуемых операций росло бы с
, делается практически невыполнимым. Таким образом, чтобы избежать этого замедления нужен алгоритм, для которого число требуемых операций росло бы с ![]() линейно, а не квадратично. В принципе такой алгоритм прост – нужно перебирать не все атомы, а только достаточно близкорасположенные. Такое утверждение представляет собой тавтологию, пока не конкретизировано понятие близкорасположенных атомов. Чтобы сделать это, разобьем ячейку моделирования на более мелкие субячейки. Тогда близкорасположенные к данному атому будут атомы, которые расположены в субячейках, соседних с субячейкой, содержащей данный атом или в субячейках соседних с соседними.
линейно, а не квадратично. В принципе такой алгоритм прост – нужно перебирать не все атомы, а только достаточно близкорасположенные. Такое утверждение представляет собой тавтологию, пока не конкретизировано понятие близкорасположенных атомов. Чтобы сделать это, разобьем ячейку моделирования на более мелкие субячейки. Тогда близкорасположенные к данному атому будут атомы, которые расположены в субячейках, соседних с субячейкой, содержащей данный атом или в субячейках соседних с соседними.
Удобно разбить ячейку моделирования на субячейки – параллелепипеды (прямоугольники в двумерном случае). Вследствие сильного отталкивания на малых расстояниях, атомы не могут подходить близко друг к другу. Поэтому можно выбрать такие размеры субячеек, что в каждой из них будет находится не более одного атома.
Таким образом, алгоритм поиска атомов, удаленных от данного атома на расстояние не больше радиуса обрезания ![]() , выглядит следующим образом. По номеру атома находим координаты атома и по ним субячейку, в которой находится атом. Затем находим субячейки, удаленные от нее на расстояние не более чем
, выглядит следующим образом. По номеру атома находим координаты атома и по ним субячейку, в которой находится атом. Затем находим субячейки, удаленные от нее на расстояние не более чем ![]() . Атомы, расположенные в этих субячейках, и будут искомыми (см. рис.1). Чтобы найти номер атома, хранящегося в заданной субячейке, удобно ввести массив, каждый элемент которого соответствует определенной субячейке. В этом элементе массива будет хранится номер атома, расположенного в этой субячейке, или нуль, если субячейка пуста. Элементы этого массива обновляются на каждом шаге по времени МД. Ясно, что изложенный алгоритм обеспечивает линейный рост числа операций с ростом числа атомов
. Атомы, расположенные в этих субячейках, и будут искомыми (см. рис.1). Чтобы найти номер атома, хранящегося в заданной субячейке, удобно ввести массив, каждый элемент которого соответствует определенной субячейке. В этом элементе массива будет хранится номер атома, расположенного в этой субячейке, или нуль, если субячейка пуста. Элементы этого массива обновляются на каждом шаге по времени МД. Ясно, что изложенный алгоритм обеспечивает линейный рост числа операций с ростом числа атомов ![]() в системе. Вариации этого алгоритма используются в программах МД “Gromex”[6], “MOLDY”[7], “DL_POLY”[8] и др.
в системе. Вариации этого алгоритма используются в программах МД “Gromex”[6], “MOLDY”[7], “DL_POLY”[8] и др.
Возможна и другая организация вычислений, которая будет удобна для организации параллельных вычислений. Именно для вычисления сил, действующих на данный атом, можно перейти от суммирования по близлежащим атомам, к суммированию по близлежащим субячейкам (см рис.1). Будем двигаться последовательно по субячейкам первого ряда. Дойдя до конца первого ряда, перейдем в начало второго ряда и т.д.
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
Рис.1 Схема поиска ближайших атомов.
Если в субячейке находится атом, то вычисляем силу, действующую на него, со стороны ближайших атомов, расположенных в близлежащих субячейках. Если же субячейка пуста, то переходим к следующей. Отметим при этом, что, например, для атома находящегося в субячейке 6 (см. рис.1) необходимо вычислить силу, действующую со стороны атомов расположенных в субячейках 1, 2, 3, 7. Силы, действующие со стороны атомов, расположенных в субячейках 5, 9, 10, 11 в силу третьего закона Ньютона, с точностью до знака уже известны. Они были вычислены, когда вычислялись силы, действующие на атомы, расположенные в этих субячейках. Таким образом, в данной организации вычислений, необходимо рассматривать лишь половину близлежайших субячеек. Далее, при переходе к смежной субячейке 7 нет необходимости исследовать все близлежащие субячейки для поиска находящихся в них близко расположенных атомов. Необходимо лишь исследовать ячейки 4 и 8. И к найденным в них атомам, добавить атомы, найденные для ячейки 6, за исключением атомов находящихся в субячейках 1 и 6. Таким образом, информация о ближайших атомах для данной субячейки не теряется, а используется при поиске ближайших атомов для смежной субячейки. Это естественно приводит к ускорению вычислений.
1.6. Периодичность
Число атомов, помещенных в ячейку моделирования, намного меньше числа атомов входящих в состав макроскопических систем. Чтобы результаты нашего моделирования можно было распространить на макроскопические тела, делают допущение, что макроскопические системы, состоят из бесконечного числа периодически повторяющихся ячеек моделирования. Такая периодичность может быть в одном, двух и трех направлениях в трехмерном случае и в одном и двух в двумерном случае (см. рис.2). В этой работе мы будем рассматривать только двумерные системы. Это связано как с повышенными требованиями к вычислительным ресурсам в случае трехмерных систем, так и с простотой визуализации результатов расчетов в двумерном случае. В двумерном случае ячейка моделирования представляет собой прямоугольник. В случае периодичности в одном направлении пара противолежащих сторон отождествляется, т.е. ячейку моделирования можно представить теперь как боковую поверхность цилиндра. В случае периодичности в двух направлениях отождествляются обе пары противоположных сторон и ячейку моделирования можно теперь представить как боковую поверхность тора. Если атом выходит за пределы ячейки моделирования, то вследствие периодичности он входит в ячейку с противоположной стороны.
1.7. Начальное состояние
В данной работе будут исследоваться с помощью МД кристаллы. Рассмотрим размещение совершенного кристалла в прямоугольной ячейке моделирования в случае периодичности в одном направлении. Периодическая структура самого кристалла накладывает ограничения на размер ячейки моделирования в направлении периодичности. Действительно, если в вершине, находящейся на одной из сторон ячейки моделирования находится атом кристалла, то эквивалентный атом кристалла должен быть в эквивалентной вершине, находящейся на другой из тождественных сторон. Это приводит к ограничениям на возможную длину ячейки моделирования в направлении периодичности и возможные ориентации кристаллографических осей кристалла относительно сторон ячейки моделирования. Возможны такие ориентации кристалла, при которых указанное выше требование выполнить точно невозможно.

Рис.2 Периодичность ячеек моделирования и размещение кристалла в ячейке моделирования.