Дипломная работа: Математична модель транспортної системи підприємства

Якщо припустити, що мережа G (V, Е) є ациклічний тобто не містить циклів, то в ній можна пронумерувати вершини так, що для кожної дуги з i у j виконується умова i < j. Очевидно, таке упорядкування може бути виконане за 0 (т) операцій. Тоді для приклада рівняння Белмана можуть бути вирішені простим обчисленням: и₁ = 0, и₂ залежить тільки від и₁ , и₃ залежить від и₁ , и₂ , иj залежить від и₁ , и₂ ,..., и_j-1 і т.д. Таким чином, рішення може бути отримане за 0 (т) операцій.

Метод Белмана - Форда. Роздивимося мережу G (V, Е), у котрої або відсутні цикли, або довжини дуг ненегативні. Метод послідовних наближень, запропонований Белманом і Фордом, складається в такому.

Нехай uj^(k) - довжина найкоротшого шляху від вихідної вершини до вершини j за умови, що шлях містить не більш ніж k дуг. Спочатку положимо

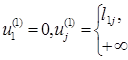
Тоді та . Для дуг k = 2, 3,...,n- 1 необхідно 0 (n) ітерацій. Кожна ітерація потребує 0 (m) операцій. Отже, метод потребує 0 (т п) операцій. Зауважимо, що для плоских графів потрібно 0 () операцій.

Він [17] запропонував модифікацію цього методу, що скорочує загальне число додавань і порівнянь приблизно в чотирьох разу у випадку повної мережі й у два рази в довільному випадку.

Задача визначення найкоротших шляхів між усіма парами вершин. Більш загальною задачею про пошук найкоротших шляхів є задача визначення найкоротших маршрутів або шляхів якнайшвидшої доставки вантажів між усіма парами вузлів транспортної мережі.

Не розглядаючи кожний з алгоритмів пошуку найкоротших шляхів, приведених у табл. 3, опишемо ідеї їхньої побудови.

Будемо шукати найкоротші шляхи між вершинами в мережі з позитивними і негативними довжинами дуг, починаючи з вершини 1. Очевидно, буде потрібно 0 (тп) обчислень для того, щоб знайти найкоротші шляхи з вершини 1 у всі інші вершини. Замінимо довжину кожної дуги на . Довжина шляху з i у j, визначена за значеннями , відрізняється від щирої довжини на константу . Отже, рішення задачі визначення всіх найкоротших пар шляхів із довжинами є рішенням вихідної задачі. Оскільки тепер усі довжини дуг невід’ємних, можна застосувати метод Дийкстра для кожній з останніх п - 1 задач. У результаті вся задача буде вирішена за 0 () операцій, а для плоского графа за 0 () операцій. У [18] запропонований алгоритм для невід’ємних дуг мережі G (V, Е), у якому очікуване число обчислень дорівнює 0 ().

Нехай мережа G (V, Е) складається з неорієнтованих дуг і ми хочемо знайти найкоротший шлях між двома визначеними вершинами. Якщо всі довжини дуг невід’ємних, те можна замінити кожну неорієнтованих дугу парою симетричних орієнтованих дуг (i,j) і (j, i) із і застосувати будь-який із зазначених вище алгоритмів.

Проте якщо довжина дуги (i,j) негативний, те цей підхід нездатний, тому що в мережі з'явиться негативний цикл (i,j), (j, i)

У загальному випадку можна скористатися, наприклад, методом Белмана- Форда для визначення існування циклу негативної довжини в G (V, Е). Якщо мережа є сильнозв`язною, то цикл негативної довжини існує тоді і тільки тоді, коли uj⁽ⁿ⁾ < uj^(n-1) для деякої вершини j. Мережа може бути перевірена на існування негативного циклу за 0 (тп) операцій.

2.2 Узагальнені задачі про потоки

У розглянутих вище задачах передбачалося, що однорідний транспортний потік, що виходить із дуги (i, j) Е, дорівнює потокові, що входить у цю дугу. Проте в ряді практичних ситуацій це припущення не виконується. Наприклад, при транспортуванні вантажів може відбуватися їхнє псування або втрата (наприклад, вивітрювання), що призводить до зменшення потоку під час його переміщення по дузі (i, j) транспортної мережі G (V, Е).

Тому для рішення подібних задач необхідно відмовитися від припущення, відповідно до якого при проходженні по дугах мережі G (V, Е) пот