Дипломная работа: Методика изучения элементов математического моделирования в курсе математики 5-6 классов

Для моделирования привлекаются различные математические объекты: числовые формулы, числовые таблицы, буквенные формулы, функции, уравнения алгебраические или дифференциальные и их системы, неравенства, системы неравенств (а также неравенств и уравнений), ряды, геометрические фигуры, разнообразные графосхемы, диаграммы Венна, графы.

?????????????? ????????????? ??????? ?????????? ??? ??????? ?????? ???????? ?????. ??? ?????????, ???????????? ?? ??????? ??????, ???????? ?? ?????????????? ???????. ?????????????, ???????? ??????????????? ? ??????????????, ??????? ??????? ? ????? ??????? ????????, ??? ??? ??????????????? ?????? ???????????? ??? ??????? (??? ???? ?? ?????????? ???????) ???????? ?????. ????? ????, ??? ?????????? ?????? ???????????? ????? ???????? ????????, ??? ?????? ????? ??????, ?????????, ?????????????, ?????????, ??????? ???????? ?????????? ????????, ? ???????????? ??? ????????. ??????????? ?????????????? ?????? ??????, ??????? ?????? ?? ???? ?????????? ????????? ??????? ???????? ? ????????????? ???????? ????????? ? ??????? ? ?? ??????? ????????????.

При решении сюжетных задач особенно часто ис­пользуются их алгебраические и аналитические модели. Такой моделью может быть функция, описывающая явление или процесс, уравнение, система уравнений, неравенство, систе­ма неравенств, система уравнений и неравенств и др. При составлении модели задача, таким образом, переводится на язык алгеб­ры или математического анализа.

Рассмотрим несколько примеров математических моделей.

Задача 1 . Турист проехал 2200 км, причем на теплоходе проехал вдвое больше, чем на автомобиле, а на поезде в 4 раза больше, чем на теплоходе. Сколько километров проехал турист отдельно на каждом виде транспорта?

Решение . Примем расстояние, которое проехал турист на автомобиле за x км. Известно, что на теплоходе проехал вдвое больше, чем на автомобиле, то есть 2x км. На поезде проехал в 4 раза больше, чем на теплоходе, то есть .

Весь путь – это сумма расстояний, которые проехал турист на каждом из видов транспорта и он равен 2200 км. Получим следующее уравнение:

- это и есть математическая модель данной задачи.

Задача 2. На школьной математической олимпиаде было предложено решить 6 задач. За каждую решенную задачу засчитывалось 10 очков, а за нерешенную снималось 3 очка. В следующий тур выходили ученики, набравшие не менее 30 очков. Сколько задач нужно было решить, чтобы попасть в следующий тур олимпиады? (См. № 151, [18]).

Решение. Пусть ученик должен решить х задач. Тогда за решенные задачи он получит 10х очков, а за 6-х нерешенных задач у него снимут 3(6-х ) очков. Ученик может получить 10х -3(6-х ) очков (все переменные выражены через выбранное х и значения других величин, заданных в задаче). По условию задачи и .

Моделью задачи служит система неравенств

.

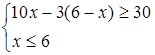Далее в качестве примера рассмотрим задачу математического анализа на нахождение экстремума. Надо заметить, что аналитической моделью задачи на наибольшее (наименьшее) значение является функция одного переменного с областью ее задания. Обычно областью задания является замкнутый промежуток.

Задача 3. Кусок проволоки длиной 48 м сгибают так, чтобы образовался прямоугольник. Какую длину должны иметь стороны прямоугольника, чтобы его площадь была наибольшей? (См. № 313, [2]).

Решение . Требуется найти размеры прямоугольника с наибольшей площадью. Обозначим за a – длину прямоугольника, тогда ширина равна .

. Полученная функция является моделью данной задачи.

Отметим, что в общем случае процесс моделирования состоит из следующих этапов:

1 этап. Постановка задачи и определение свойств оригинала, подлежащих исследованию.

2 этап. Констатация затруднительности или невозможности исследования оригинала.

3 этап. Выбор модели, достаточно хорошо фиксирующей существенные свойства оригинала и легко поддающейся исследованию.

4 этап. Исследование модели в соответствии с поставленной задачей.

5 этап. Перенос результатов исследования модели на оригинал.

6 этап. Проверка этих результатов.

На сегодняшний день наиболее распространенной является трехэтапная схема процесса мате­матического моделирования:

1) перевод предложенной задачи с естественного языка на язык математических терминов, то есть построение математической модели задачи (формали­зация);

2) решение задачи в рамках математической теории (решение внутри модели);

3) перевод полученного результата (математического решения) на язык, на котором была сформули­рована исходная задача (интерпрета­ция полученного решения).

Наиболее ответственным и сложным является первый этап – само построение математической модели. Оно осуществляется логическим путем на основе глубокого анализа изучаемого явления (процесса) и требует умения описать явление (процесс) на языке математики.

В свою очередь, в процессе построения модели можно выделить несколько шагов.

Первый шаг – индуктивный: это отбор наблюдений, относящихся к тому процессу, который предстоит моделировать. Этот этап состоит в формулировке проблемы, то есть в принятии решения относительно того, что следует принимать во внимание, а чем можно пренебречь.