Дипломная работа: Методы приближённого решения матричных игр
U1 ={a1 , a2 ,..., am } – множество стратегий первого игрока;
U2 ={b1 , b2 , ... bn } – множество стратегий второго игрока.
Будем называть эти стратегии чистыми в отличие от смешанных, которые будут введены далее.
Множество U1 ×U2 – декартово произведение множеств стратегий игроков называется множеством ситуаций в игре. Для каждой ситуации должен быть определён итог игры. Так как игра антагонистическая достаточно определить выигрыш а одного из игроков, скажем первого. Тогда выигрыш второго игрока будет равен (-а ). Таким образом, имеем матрицу выигрышей первого игрока ( для второго игрока матрица выигрышей будет -А):
![]() A=
A= 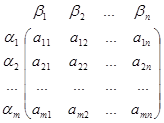
Определение. Система Г={ U 1 , U 2 , A } называется матричной игрой двух лиц.
Разыгрывание матричной игры сводится к выбору игроком 1 i-ой строчки матрицы выигрышей, а игроком 2 - j-го столбца. После этого игрок 1 получает выигрыш равный а ij , а игрок 2 – (-а ij ).
При правильной игре игрок 1 может всегда гарантировать себе выигрыш, который назовём нижним значением цены игры. Обозначим его: ![]() .
.
В свою очередь, игрок 2 может гарантировать себе проигрыш, который назовём верхним значением цены игры. Обозначим его:
![]() .
.
Чистые стратегии i* и j* , соответствующие ![]() называются максиминной и минимаксной стратегиями.
называются максиминной и минимаксной стратегиями.
Лемма 1. В матричной игре ![]() . [17]
. [17]
Определение. Ситуация ( i * , j * ) называется ситуацией равновесия, если для i Î 1,2,…, m , j Î 1,2,…, n выполняется неравенство:
![]() .
.
Ситуация равновесия это такая ситуация, от которой ни одному из игроков не выгодно отклоняться. В этом случае стратегии i* , j* называют оптимальными стратегиями игроков.
Чтобы такая ситуация существовала необходимо и достаточно равенство верхней и нижней цен игры, т. е. ![]() .[17]
.[17]
Определение. Пусть( i * , j * ) - ситуацией равновесия в матричной игре. Тогда число ![]() называется значением или ценой игры.
называется значением или ценой игры.
Например, в игре ГА с матрицей А=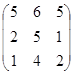 существует не одна ситуация равновесия. В данной игре их две: (1, 1) и (1, 3).
существует не одна ситуация равновесия. В данной игре их две: (1, 1) и (1, 3).
Множество всех ситуаций равновесия в матричной игре обозначим через Z(Г).
Лемма о масштабе 1. Пусть Г и Г/ - две матричные игры с матрицей выигрышей А={ aij } и A / ={ a / ij }, причём А/ = b А+ a , b = const , a = const .
Тогда Z (Г)= Z (Г/ ) и n / = b n + a (где n / - значение цены игры Г/ , n - значение цены игры Г). [17]
Эта лемма имеет большое практическое значение, так как большинство алгоритмов для решения матричных игр основано на предположении, что матрица игры положительна. В случае, когда матрица имеет неположительные элементы, следует прибавить ко всем элементам матрицы число наибольшее по абсолютной величине, из всех отрицательных элементов.
Существуют игры, в которых ситуации равновесия в чистых стратегиях не существует. Тогда игрокам бывает не выгодно придерживаться своих минимаксных и максиминных стратегий, так как они могут получить больший выигрыш, отклонившись от них. В этом случае игрокам разумно действовать случайно, т. е. выбирать стратегии произвольно и не сообщать о выборе сопернику. Такие стратегии игроков будем называть смешанными.
Определение. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.
Так если игрок 1 имеет m чистых стратегий, то его смешанная стратегия x – это набор чисел x =( x 1 , x 2 ,…, xm ), которые удовлетворяют соотношениям ![]() ,
, ![]() =1. Аналогичным образом определяется смешанная стратегия y игрока 2.
=1. Аналогичным образом определяется смешанная стратегия y игрока 2.
Определение. Оптимальными стратегиями игроков называются стратегии, которые при многократном повторении обеспечивают игрокам максимально возможный средний выигрыш (или минимально возможный средний проигрыш).
Таким образом, процесс игры при использовании игроками своих смешанных стратегий превращается в случайное испытание, которое назовём ситуацией в смешанных стратегиях. Она обозначается так ( x , y ), гдеx и y – смешанные стратегии игроков 1 и 2 соответственно.
Для ситуации в смешанных стратегиях каждый игрок определяет для себя средний выигрыш, который выражается в виде математического ожидания его выигрышей:![]() .
.
От матричной игры пришли к новой игре ![]() ={X, Y, K}, где X, Y – множества смешанных стратегий игроков, а K – функция выигрышей в смешанных стратегиях. Такую игру называют смешанным расширением матричной игры.
={X, Y, K}, где X, Y – множества смешанных стратегий игроков, а K – функция выигрышей в смешанных стратегиях. Такую игру называют смешанным расширением матричной игры.
Цели игроков остаются прежними: игрок 1 желает получить максимальный выигрыш, а игрок 2 стремится свести свой проигрыш к минимуму. Поэтому для смешанного расширения игры, аналогичным образом определяются верхнее и нижнее значение цены игры, только теперь игроки выбирают свои смешанные стратегии. Обозначим их:
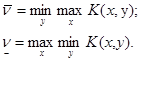
В этом случае остаётся справедливой лемма 1, т. е.![]() .
.
Определение. Ситуация ( x * , y * ) в игре образует ситуацию равновесия, если для всех x Î X , y Î Y выполняется равенство:
K ( x , y * )≤ K ( x * , y * )≤ K ( x * , y ).
Чтобы ситуация равновесия в смешанном расширении игры существовала необходимо и достаточно равенство верхней и нижней цен игры, т. е. ![]() , где n - цена игры.
, где n - цена игры.