Дипломная работа: Методы приближённого решения матричных игр
Лемма о масштабе 2.
Пусть ГА и ГА / - две матричные игры А/ = a А+ В, , a = const , В – матрица с одинаковыми элементами b , т. е. b ij = b для всех i , j .
Тогда Z (![]() )= Z (ГА / ) и n А / = a n А + b (где n А / - значение цены игры ГА / , n А - значение цены игры ГА ). [17]
)= Z (ГА / ) и n А / = a n А + b (где n А / - значение цены игры ГА / , n А - значение цены игры ГА ). [17]
Теорема. В смешанном расширении матричной игры всегда существует ситуация равновесия. [17]
§2. Итеративный метод Брауна-Робинсона (метод фиктивного разыгрывания)
Часто в практических задачах нет необходимости находить точное решение матричной игры. Достаточно найти приближённое решение, которое даёт средний выигрыш, близкий к цене игры и приближённые оптимальные стратегии игроков.
Ориентировочное значение цены игры может дать уже простой анализ матрицы выигрышей и определение нижней и верхней цен игры. Если они близки, то поисками точного решения заниматься не обязательно, так как достаточно выбрать чистые минимаксные стратегии. Если же они не близки, можно получить приемлемое для практики решение с помощью численных методов решения игр, из которых рассмотрим метод итераций.
Пусть разыгрывается матричная игра ГА с матрицей А={aij } размера (m´n). Идея метода – многократное фиктивное разыгрывание игры с заданной матрицей. Одно разыгрывание игры будем называть партией, число которых неограниченно.
В 1-ой партии оба игрока выбирают совершенно произвольные чистые стратегии. Пусть игрок 1 выбрал i-ю стратегию, а игрок 2 – j-ю стратегию. Во второй партии игрок 1 отвечает на ход игрока 2 той своей стратегией, которая даёт ему максимальный выигрыш. В свою очередь, игрок 2, отвечает на этот ход игрока 1 своей стратегией, которая обращает его проигрыш в минимум. Далее третья партия.
С ростом числа шагов процесса смешанные стратегии, которые приписываются игрокам, приближаются к их оптимальным стратегиям. Этот процесс приближённого нахождения оптимальных стратегий игроков называется итеративным , а его шаги – итерациями.
Итак, предположим, что за первые kразыгрываний игрок 1 использовал i-ю чистую стратегию ![]() i k раз (i=1,…,m), а игрок 2 j-ю чистую стратегию
i k раз (i=1,…,m), а игрок 2 j-ю чистую стратегию ![]() раз (j=1,…,n). Тогда их смешанными стратегиями будут векторы
раз (j=1,…,n). Тогда их смешанными стратегиями будут векторы ![]() .
.
Игрок 1 следит за действиями игрока 2 и с каждым своим ходом желает получить как можно больший выигрыш. Поэтому в ответ на применение игроком 2 своей смешанной стратегии y k , он будет использовать чистую стратегию ik +1 , которая обеспечит ему лучший результат при разыгрывании (k+1)-ой партии. Игрок 2 поступает аналогично. В худшем случае каждый из них может получить:
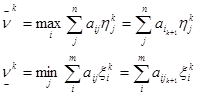
где ![]() - наибольшее значение проигрыша игрока 2 и
- наибольшее значение проигрыша игрока 2 и ![]() - наименьшее значение выигрыша игрока 1.
- наименьшее значение выигрыша игрока 1.
Рассмотрим отношения, которые определяют средние значения проигрыша игрока 2 и выигрыша игрока 1:
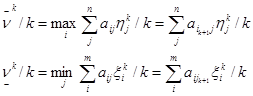
Пусть ν - цена матричной игры ГА . Её значение будет больше выигрыша игрока 1, но меньше проигрыша игрока 2, т. е.
![]() . (1)
. (1)
Таким образом, получен итеративный процесс, позволяющий находить приближённое решение матричной игры, при этом степень близости приближения к истинному значению игры определяется длиной интервала
![]() .
.
Сходимость алгоритма гарантируется следующей теоремой.
Теорема. ![]() .
.
Схема доказательства.
Лемма. Для всякой матрицы А и " e > 0 существует такое k 0 , что
![]() .
.
При предельном переходе в неравенстве (1) при k®¥имеем:
![]() . (2)
. (2)
Отсюда получаем оценку разности пределов:
![]() .
.
Из леммы следует, что
![]() .
.
На основании неравенства (1) имеем:  .
.
Следовательно, в силу ограниченности пределов
![]() .
.
Получаем оценку для разности пределов:
![]() для "e>0.
для "e>0.
Можем заключить, что ![]() . Осталось показать равенство пределов n . Это следует из неравенства (2).
. Осталось показать равенство пределов n . Это следует из неравенства (2).