Дипломная работа: Модель портального манипулятора

или через проекции на оси неподвижной системы осей в виде

.

(1.12)

По аналогии с введем вектор угловой скорости звена

(1.13)

и запишем равенство (1.6) в развернутой форме для случая, когда звенья манипулятора обладают симметрией относительно главных осей инерции. Для этого подставим выражения , , из (1.7), (1.11), (1.13) в (1.6) и получим

.

(1.14)

При использовании вектора скорости центра инерции в форме (1.14) выражение

,

(1.15)

с учетом которого равенство (1.4) принимает вид

.

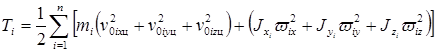(1.16)

Построение динамической модели переходных процессов манипулятора МРЛ-901П

Модель переходных процессов в манипуляторе МРЛ-901П

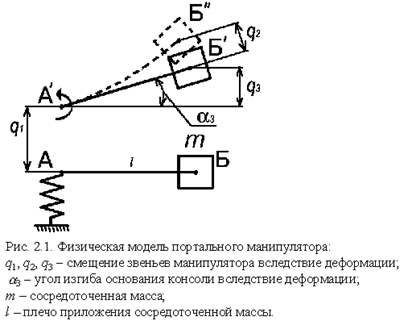
Модель портального манипулятора МРЛ-901П представлена на рис. 2.1. Деформирующимися элементами в манипуляторе являются: зубчатый ремень, обозначенный пружиной; консольная часть, на которой имеется сосредоточенная масса m . Деформация поперечной консоли обозначена на схеме углом . Исходными данными для расчета такой модели будут: значение подвижной массы m , плечо приложения этой массы l , а также коэффициент натяжения зубчатого ремня, определяемый как отношение прогиба ремня к его длине и влияющий на жесткость, и демпфирование модуля линейного перемещения.

При остановке электроприводов подвижные массы будут продолжать движение под действием инерционных сил, в результате чего точки А и Б займут положение и соответственно, затем остановятся и под действием сил упругой деформации пружины и балки начнут совершать колебательное движения.

Рассматриваемая модель имеет три степени свободы, обозначим независимые обобщенные координаты как , и . Для описания данной модели воспользуемся уравнением Лагранжа второго рода:

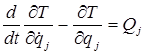(j = 1,2,…,k ),

(2.1)

где T - кинетическая энергия системы; Q - обобщенная сила; k - количество степеней свободы.

Кинетическая энергия системы с тремя степенями свободы является однородной квадратичной формой обобщенных скоростей [5]:

,

(2.2)

Коэффициенты являются функциями координат , и .

Предположим, что обобщенные координаты отсчитываются от положения равновесия, где .

Располагая коэффициенты по степеням и пологая для упрощения записи , получим:

(2.3)

Потенциальная энергия системы:

(2.4)

При этом учитываем, что в положении равновесия обобщенные силы также обращаются в нуль.

В (2.4) для упрощения приняты следующие обозначения:

, , , , , .

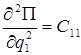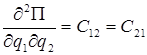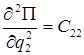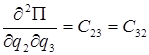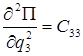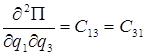Для составления дифференциальных уравнений свободных колебаний в форме уравнений Лагранжа второго рода, выразим потенциальную энергию через обобщенные координаты. Рассмотрим равновесие системы, на которую действуют силы …,. Потенциальная энергия в состоянии устойчивого равновесия имеет минимум, равный нулю, а при вызванном действием сил отклонении от него выражается квадратичной формой вида (2.4).

Элементарная работа всех сил действующих на систему, по принципу возможных перемещений должна быть равна нулю:

.

(2.5)

Замечая, что

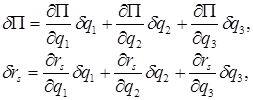а также приравнивая к нулю коэффициенты при независимых вариациях , и , получаем три уравнения:

,

(2.6)

Здесь , и - обобщенные силы для системы сил …,, уравновешивающих потенциальные силы, возникающие при отклонении системы из положения равновесия . Заменяя в (2.6) производные потенциальной энергии их выражениями согласно (2.4), получим систему уравнений, определяющих значение координат , и в положении равновесия:

,

(2.7)

причем , и .

Решение системы (2.7) имеет вид:

,

(2.8)

где

(2.9)

.

На систему действуют обобщенные силы, которыми являются инерционные силы и силы сопротивления движению. Обычно в сложных системах в целях упрощения [4, 5] силу сопротивления принимают пропорциональной первой степени скорости движения. С целью упрощения условимся, что угол мал и координаты массы m можно записать как . Поэтому на основании кинетостатики можем записать:

,

(2.10)