Дипломная работа: Насыщенные формации заданной структурой подформаций

В настоящее время теория насыщенных формаций является весьма развитым учением, обогащенным большим числом ярких теорем и содержательных примеров. Они отражены в ряде работ. В то же время, частично насыщенные формации и, в частности, -насыщенные формации изучены сравнительно мало. Следует отметить, что как показывают результаты ряда авторов, полученные в последние годы, -насыщенные формации весьма полезны при анализе многих вопросов при исследовании нормального строения конечных непростых групп. А методы, разработанные на основе частично насыщенных формаций широко используются в различных областях современной математики. Наиболее широкий диапазон применения этой теории в общей алгебре.

Настоящая дипломная работа посвящена изучению свойств частично насыщенных формаций с заданной структурой подформаций. Работа состоит из перечня условных обозначений, реферата, введения, основной части, включающей три раздела, заключения и списка цитируемой литературы. Каждый раздел условно можно разделить на две части. Первая часть носит вспомогательный характер. В ней приводятся обозначения, определения понятий, которые неоднократно используются в дальнейшем. В этой части также включены некоторые результаты теории формаций конечных групп для удобства ссылок и независимости текста работы от других источников. Во второй части работы находятся новые результаты, полученные автором в результате изучения данной темы.

Первый раздел посвящен изложению основных свойств решетки -насыщенных формаций. Здесь собраны из различных источников и систематизированы основные результаты о частично насыщенных формациях и их -локальных спутниках. Доказано, что совокупность всех внутренних -локальных спутников формации образует полную модулярную решетку.

Во втором раздле дипломной работы исследуется -дефект -насыщенной формации. Изучаются вопросы, связанные с понятием минимальных -насыщенных не -нильпотентных подформаций. Основным результатом этого раздела является теорема , дающая описание -насыщенных формаций -нильпотентного дефекта .

В третьем разделе рассматриваются -насыщенные формации, у которых решетка -насыщенных формаций, заключенных между и , является решеткой с дополнениями. В теореме получено описание -насыщенных формаций такого вида.

Работа носит теоретический характер. Результаты ее могут быть использованы в учебном процессе при чтении спецкурсов на математических специальностях в высших учебных заведениях.

1. Решетка всех 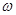-насыщенных формаций и ее основные свойства

Спутники формаций

В работе рассматриваются только конечные группы. Используются определения и обозначения, принятые в книгах - и работе .

Напомним, что через обозначают множество всех простых чисел. Пусть - некоторое непустое множество простых чисел. - дополнение к во множестве простых чисел, т.е. . Через обозначают множество всех различных простых делителей натурального числа , а через - множество всех простых делителей порядка группы , т.е. . Полагают также, что . Натуральное число называется -числом , если . Группа называется -группой , если ее порядок есть -число.

Определение.Формация - это класс групп, замкнутый относительно гомоморфных образов и конечных подпрямых произведений, т.е. - формация, если

1) и следует, что ;

2) и следует, что .

Напомним, что если - произвольный непустой класс групп, то через обозначают пересечение всех формаций, содержащих .

Определение.Пусть - непустое множество простых чисел. Всякую функцию вида

называют -локальным спутником . При этом запись означает множество .

Для произвольного класса групп символом обозначают пересечение всех таких нормальных подгрупп , что , а символом обозначают произведение всех нормальных -подгрупп группы .

Пусть - класс всех тех групп, у которых каждый композиционный фактор является -группой.

Полагают, , .

Через обозначают наибольшую нормальную -подгруппу группы .

Лемма. Пусть - нормальная подгруппа группы .

1. Если - -группа, то .

2. Если , то .

Для произвольного -локального спутника

Лемма. Пусть , где и . Тогда либо , либо найдется такое число , что .

Доказательство. Пусть и для всех . Первое соотношение влечет . Пусть . Тогда и . Значит, для всех имеет место включение . Следовательно, . Полученное противоречие доказывает лемму.

Определение.Если формация такова, что , то говорят, что является -локальной , а - ее -локальный спутник . Если при этом все значения таковы, что для любого , то называется внутренним -локальным спутником .

Пример. Пусть - формация, содержащаяся в , и - такой -локальный спутник, что и для любого . Тогда, очевидно, . Таким образом, всякая подформация формации является -локальной. Отсюда, в частности, следует, что пустая формация и формация единичных групп являются -локальными для всех .

Определение.Насыщенной называют такую формацию , что для любой группы с всегда следует .

Определение.Формацию называют -, если ей принадлежит всякая группа , для которой , где . В частности, если , то -насыщенные формации называют -насыщенными .