Дипломная работа: Оборудование минипекарень

где a_теста - коэффициент теплоотдачи поверхности тестовых заготовок;

S_теста - площадь поверхности тестовых заготовок;

Т_теста - температура тестовых заготовок, скорость изменения которой, с учетом того, что при расстойке в тестовых заготовках выделяется энергия Q_{теста выд} , составляет:

,

где c_теста - теплоемкость тестовых заготовок;

m_теста - масса тестовых заготовок.

Аналогично, тепловой поток, получаемый тележками и используемый для их прогрева, также может быть описан формулой конвективного теплообмена:

Q_тел = a_тел ´ S_тел ´ (Т_возд - Т_тел ),

где a_тел - коэффициент теплоотдачи поверхности тележек;

S_тел - площадь поверхности тележек;

Т_тел - температура тележек, скорость изменения которой:

,

где c_тел - теплоемкость тележек;

m_тел - масса тележек.

Потери теплоты через стенки расстойного шкафа рассчитываются по уравнению теплопередачи:

Q_ст = k_cт ´ S_ст ´ (Т_возд - Т_ос ),

где k_ст - коэффициент теплопередачи через стенки;

S_ст - площадь стенок камеры расстойного шкафа;

Т_ос - температура окружающей среды.

Следует учесть, что коэффициенты теплоотдачи конвекцией (a_тэн , a_теста , a_тел ) и коэффициент теплопередачи k_ст (также зависящий от коэффициентов теплоотдачи поверхностей стенок) в свою очередь зависят от многих факторов: от температур поверхностей и омывающей их среды, от скорости движения последней, от ее теплопроводности, вязкости, плотности и теплоемкости (в свою очередь также зависящих от температуры среды), от конфигурации и состояния поверхностей и их геометрических размеров. Нахождение коэффициентов теплоотдачи конвекцией возможно путем решения системы дифференциальных уравнений (Фурье-Кирхгофа, Навье-Стокса, сплошности(непрерывности), дифференциального уравнения теплообмена, описывающего процесс теплоотдачи на границах тела) с прибавлением краевых условий (геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс теплопередачи; физические условия, характеризующие физические свойства среды и тела; граничные условия, характеризующие протекание процесса теплопередачи на границах тела; временные условия, характеризующие протекание процесса во времени). Это возможно лишь в некоторых частных случаях при использовании ряда упрощений, причем полученные решения не всегда согласуются с опытными результатами. Поэтому изучение конвективного теплообмена развивалось, как правило, экспериментальным путем. Однако чисто экспериментальное изучение какого-либо физического явления имеет тот недостаток, что его результаты имеют ограниченную ценность, так как применимы лишь к частному явлению. Это чрезвычайно усложняет эксперимент, заставляя опытным путем проверить зависимость данного явления от ряда факторов, а некоторые явления зависят от многих переменных. На помощь в этих случаях приходит теория подобия, позволяющая в известной степени обобщить полученные опытные результаты, распространить их на целую группу подобных явлений. Подобные системы характеризуются безразмерными комплексами, составленными из характеризующих явление величин, сохраняющими одно и то же численное значение. Такие величины носят название инвариантов или критериев подобия и обозначаются символами, состоящими из первых букв фамилий ученых, которые их ввели в употребление или вообще работали в данной области. Для определения критериев теплового подобия для передачи тепла в движущейся среде конвекцией используется дифференциальное уравнение теплопроводности Фурье-Кирхгофа совместно с граничным уравнением теплообмена. На основе уравнения подобия процессов определяются соотношения между постоянными подобия, и из которых путем подстановки определяются критерии теплового подобия:

Nu = a´ l / l - число Нуссельта.

Число Нуссельта характеризует собой условия теплопередачи между твердым телом и средой, оно содержит в себе искомую величину - коэффициент теплоотдачи a, коэффициент теплопроводности среды l и определяющий размер l, характеризующий собой геометрическое подобие.

Ре = u´ l / a - число Пекле.

Число Пекле обычно преобразуется и представляется в виде двух критериев:

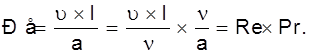
Число Рейнольдса Re содержит в себе скорость потока u и коэффициент кинематической вязкости n = m/r м² /с, где m - коэффициент динамической вязкости, характеризует собой ее внутреннее трение; r - плотность среды. Число Рейнольдса является критерием гидродинамического подобия, он характеризует собой условия вынужденного движения среды.

Множителями числа Прандтля Pr являются физические параметры - кинематическая вязкость и коэффициент температуропроводности - число Прандтля характеризует собой свойства среды. Оно практически не зависит ни от давления, ни от температуры. Так как коэффициент температуропроводности

a = l / (c ´r ),

то Pr = c ´r´n / l ,