Дипломная работа: Обработка изображений на основе аналоговых нейрокомпьютеров

НФП позволяет реализовать неалгоритмический принцип вычислений (НПВ) путем ввода в машину и реализации решения задачи в общепринятой аналитической форме ее описания. Аналитический принцип обработки информации состоит в том, что каждой аналитической завимости между математическими переменными исходной задачи (интегродифференциальной, алгебраической, тригонометрической и т.п.) в машине соответствуют аналогичное (подобное) аналитическое описание связи между машинными переменными. Это достигается методом моделирования на основе теории подобия.

Наиболее распространенный НПВ – аналоговое математическое моделирование по методу непрямой аналогии, основанному на операционно-блочном построении модели, когда каждой операции и функции уравнений исходного оригинала в модели соответствует подобный операционный блок (сумматор, интегратор, блок умножения и деления, функциональный преобразователь и т.п.). Используя достаточный набор типовых операционных блоков, можно решать широкий класс математических задач. Программирование аналоговых вычислительных машин (АВМ) заключается в составлении схемы аналоговой модели, представляющей собой схему соединения друг с другом типовых операционных блоков в соответствии с заданной задачей, и в расчете настраиваемых параметров операционных блоков, так называемом масштабировании модели.

Например, нелинейное неоднородное обыкновенное дифуравнение второго порядка:

при начальных условиях:

может быть запрограммировано к решению на АВМ следующим способом.

Схема аналоговой модели составляется методом понижения порядка (выделением высшей производной и последовательным её интегрированием) и методом неявных функций, условно полагая искомые якобы вначале известными:

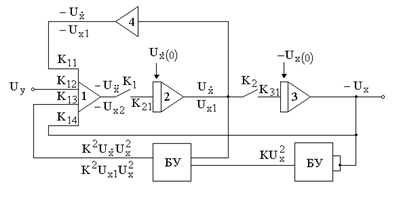
Блок 1 – аналоговый сумматор со стандартным оператором:

Блок 4 – инвертор с оператором: .

Блоки 2,3 – аналоговые интеграторы со стандартным оператором:

.

Блок БУ – аналоговый блок умножения с оператором: , где

k – коэффициент нормирования шкалы выходного напряжения:

,

а - предельное значение шкалы на выходе операционного блока (в АВМ типа МН – 7).

Решение дифференциального уравнения начинается в момент времени t=0 синхронного замыкания пусковых ключей К1, К2 на входах интеграторов и завершается по окончании переходных процессов. Следовательно, в процессе вычислений все операционные блоки модели функционируют параллельно и одновременно. Этим и объясняется возможность повышения производительности на основе НПВ.

В исходном состоянии модели при разомкнутых ключах К1, К2 выполняется подготовка АВМ: ввод значений коэффициентов передачи (КП) К11,…, К14, К21, К31 и начальных условий, соединение операционных блоков по схеме модели.

Масштабирование модели состоит в расчете КП: К11,…, К14, К21, К31; НУ: и машинной переменной правой части Uy с учетом масштабов переменных. Оно заключается в выводе масштабных уравнений модели на основе сопоставления сходственных систем уравнений оригинала и модели.

Уравнения оригинала со вспомогательными переменными х1, х2 и обязательной нормировкой величины коэффициентов в левой части уравнений К=1:

Уравнения модели как совокупность стандартных операторов операционных блоков (при выводе масштабных уравнений начальные значения интегралов вначале не учитываются.):

Уравнения модели, преобразованные в сходственную с оригиналом дифференциальную форму:

Уравнения модели, преобразованные путем замены машинных величин на математические величины оригинала с учетом их масштабов: