Дипломная работа: Производство химических волокон

Уравнения движения в цилиндрической системе координат (r,Ө,z):

В компонентах тензора напряжений первый индекс указывает направление нормали к площадке, на которой действует данное напряжение, второй индекс - направление действия напряжения.

В силу симметрии тензора напряжений справедливы следующие равенства (закон парности касательных напряжений):

Приведенные выше уравнения движения не описывают связи между величиной напряжения сдвига и соответствующими скоростей деформации. Для того чтобы полностью охарактеризовать поведение деформирующего полимера, необходимо дополнить это уравнение реологическим уравнением состояния, связывающим компоненты тензора скоростей деформации с компонентами тензора напряжений.

Из реологического уравнения, которое относится к случаю установившегося одномерного течения.

Реологическое уравнение состояния, учитывающее релаксационный характер развития высокоэластической деформации и справедливо при малых обратных деформациях, имеет вид:

где

Заметим, что уравнения состояния следует связывать для определенного интервала времени не с какой-либо определенной точкой пространсва с координатами х ⁱ , а с одним и тем же элементом среды, находившимся в момент времени t в точке пространства с координатами х ⁱ .

В последнее время так же популярна формула реологического состояния для упруговязской среды предложенная Уайтом.

где pI- изотропия составляющая тензора напряжений.

Функционал G можно представить в виде интегрального разложения:

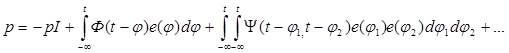
Реологические свойства среды определяются соответствующим выбором интегральных ядер Ф и Ψ. Первое ядро Ф связывает релаксационный модуль линейной вязкоэластичности и ограничивает область малых деформация.

Используя некоторое мгновенное состояние среды как начало отсчета, можно выразить конкретную деформацию среды при помощи разложения в ряд Тейлора:

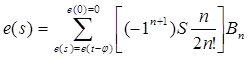
где - e (s) =e (t- φ) - тензор деформаций, определенных в соответствии с мерой Финглера:

Простейшая форма реологического уравнения, учитывающая аномалию вязкости:

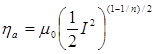
где I₂ - квадратичный инвариант тензра скоростей деформации,

μ₀ - значение эффективной вязкости при I₂ =1.

Значение квадратичного инварианта в прямоугольных координатах:

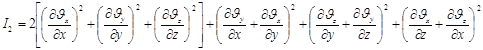
Значение квадратичного инварианта в цилиндрических координатах: