Дипломная работа: Производство химических волокон
в случае простого сдвига реологическое уравнение примет вид:

Уравнение энергетического баланса, составленное для установившегося режима в предположении, что все теплофизические характеристики не зависят от температуры, имеет вид:
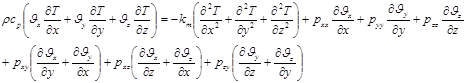
где ρ - плотность расплава, С p - теплоемкость расплава, km - коэффициент теплопроводности расплава.
Для построения модели, допускающей аналитическое решение, сделаем следующие допущения:
Течение в направлении оси y существует только в непосредственной близости к стенкам канала. В остальной части сечения канала течение в направлении оси y отсутствует ![]() .
.
Размеры канала по всей дине постоянны, следовательно, значения υx и υz не зависят от z .
Температурный градиент в поперечном направлении из-за циркуляционного течения пренебрежимо мал по сравнению с продольным градиентом. Таким образом, ![]()
Если уравнение энергетического баланса будем считать, что теплопередача за счет теплопроводности за счет вдоль оси канала пренебрежимо мала, то уравнение энергетического баланса сведется к следующему виду:
![]()
3.1 Формования комплексных нитей из расплава
Принцип формования комплексных нитей из расплава заключается в продавливании расплава полимера с помощью дозирующего насоса через тонкие отверстия фильеры. Выходящая из каждого отверстия фильеры струйка расплава полимера, охлаждаясь на воздухе, затвердевает и превращается в элементарную нить. Соединенные в пучок элементарные нити образуют комплексную нить, которая наматывается на бобину.
Фильеры обычно представляют собой короткие капилляры, у которых ![]() . Канал фильеры имеет плавный контур, что позволяет придать потоку на входе форму рюмки и свести до минимума искажение формы экструдата, обусловленным эластическим восстановлением.
. Канал фильеры имеет плавный контур, что позволяет придать потоку на входе форму рюмки и свести до минимума искажение формы экструдата, обусловленным эластическим восстановлением.

Рисунок 1 - Схема формования волокна из расплава
С увеличением скорости вытяжки и ориентационного напряжения величина отношения D/ D0 быстро уменьшается. Приблизительное выражение для оценки эластичного восстановления струи при наличии вытяжки имеет следующий вид:
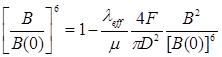
где, B= D/ D0 - коэффициент восстановления струи осевом усилии,
F = 0, λeff - время релаксации макромолекул расплава полимера ![]() ,
,
μ - условно фиксированный динамический коэффициент вязкости,
G - функция, описывающая диссипацию внутренней энергии потока.
По степенному закону Освальда де Виля следует, уравнение сохранения энергии и количества движения следующие:
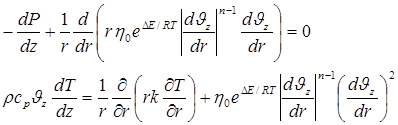
При рассмотрении энергетического баланса интенсивность теплового потока за счет работы сил вязкого трения, отнесенная к единице обьема (ev ) описывается выражением:
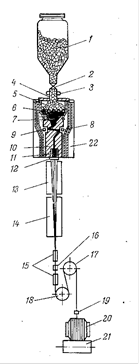
Рисунок 2 - Прядильное место: 1 - бункер с крошкой; 2 - кран; 3 - компенсатор; 4 - патрубок; 5 - плавильная решетка; в - паровая рубашка; 7-расплавленный полимер; 8-дозирующий насос; 9 - напорный насос; 10 - насосный блок; 11 - фильерный комплект; 12 - фильера; 13 - обдупоч-ная шахта; 14 - прядильная шахта; 15 - препарационпые шайбы; 16 - прижимной ролик; 17 и 18 - прядильные (приемные) лиски; 19 - ннтераскладчик; 20-шпуля; 21 - фрикционный цилиндр; 22 - теплоизоляция.
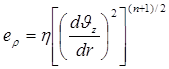
где − ![]()
Для формования нитей из расплава характерна вертикальная схема при движении нити сверху вниз. Машина для формования капроновых нитей комплектуется из ряда прядильных мест. Каждое прядильное место (рис.2) состоит из трех основных узлов: узла плавления поликапроамида (крошки) и нитеобразования. Зоны отверждения струек расплава и образования элементарных и комплексной нитей. Устройства для намотки сформованной комплексной нити.