Дипломная работа: Радиолокационные установки
.
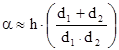Выражение (1.28) может быть аппроксимировано с использованием безразмерного дифракционного параметра Френеля - Кирхгофа:
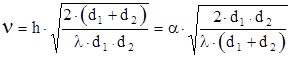, (1.29)
где a подставляется в радианах, все остальные параметры - в метрах. Таким образом, разность фаз Ф может быть вычислена из выражения
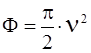. (1.30)
Из выражения (1.30) следует, что сдвиг фазы между прямым и дифракционным лучами является функцией высоты h и взаимного расположения препятствия, излучателя и приемника.
Дифракционные потери мощности в радиоканале могут быть объяснены с помощью зон Френеля. Зоны Френеля представляют собой области, разность хода через которые от излучателя до приемника составляет nl/2 по сравнению с прямым лучом (l - длина волны, n - целое число).
В мобильной связи обычно наблюдается затенение части зон (источников вторичных волн) и, следовательно, уменьшение доли принятой мощности. В зависимости от геометрии препятствия принятая энергия определяется через векторное суммирование вторичных волн.
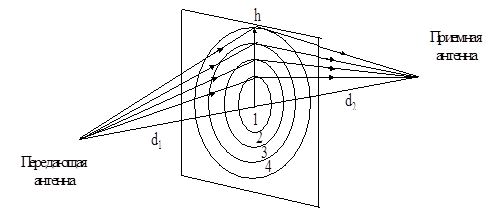
Рис.1.6 Формирование зон Френеля
Если препятствие не затеняет первую зону Френеля, то дифракционные потери минимальны и ими пренебрегают. Используют следующее свойство: если открыто не менее 55% первой зоны Френеля, то дальнейшее открытие первой зоны Френеля не уменьшает дифракционные потери.
1.3.2 Модель дифракции радиоволн на одиночном клине
Определение степени ослабления поля холмами и зданиями является достаточно сложной задачей при расчете зон обслуживания. Обычно точный расчет ослабления невозможен, поэтому используют методы расчета поля с необходимыми экспериментальными поправками.
Препятствие в виде одиночного холма или горы может быть обсчитано с использованием модели клина. Это простейшая модель препятствия, и быстрый расчет ослабления возможен с использованием классического решения Френеля для дифракции поля на полуплоскости.
Рис.1.7 Варианты перекрытия видимости антенн препятствием
Напряженность поля в точке расположения приемной антенны определяется векторной суммой вторичных источников, лежащих в плоскости, расположенной над препятствием. Напряженность поля при дифракции на клине определяется выражением
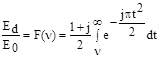, (1.31)
где Е0 - напряженность поля в точке расположения приемной антенны при отсутствии препятствия и земли, а F (n) - комплексный интеграл Френеля. Значение интеграла F (n) определяется из графиков и таблиц.
Коэффициент дифракционного усиления с препятствием (обычно он меньше 1) по сравнению со свободным пространством
, дБ. (1.32)
График этой функции показан на рис.1.8
Gd , дБn
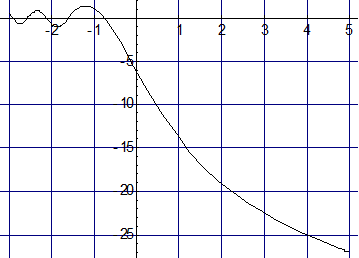
Рис.1.8 Зависимость коэффициента дифракционного усиления от значения параметра дифракции n
Приближенно можно считать:
(1.33a)
(1.33б)
(1.33в)
(1.33г)