Дипломная работа: Разработка математической модели и ПО для задач составления расписания
(11)

Введенная целевая функция не является единственно возможной. Введение других целевых функций не меняет ограничений математической модели и методов решения задачи, но может существенно повлиять на результаты вычислений.
2.2. ?????? ??????? ???????????? ??????Поставленная в предыдущем пункте задача максимизации линейной целевой функции при заданной системе ограничений является задачей линейного целочисленного булева программирования, поскольку все коэффициенты ограничений целочисленны в силу дискретности исходных данных задачи; кроме этого искомые переменные математической модели могут принимать только два значения. На данный момент времени существует несколько возможных методов решения такого рода задач.
В [3] – [8] описаны методы упорядоченной индексации и модифицированных пометок, основанные на лагранжевой декомпозиции исходной модели на ряд однострочных задач, решаемых соответственно методами упорядочивающей индексации или модифицированных пометок. К сожалению количество операций каждого из методов не допускает полиномиальной оценки; кроме того, размерность таблицы наборов (промежуточных значений) методов резко возрастает при увеличении размерности решаемой задачи, что недопустимо в нашем случае. Возможно, изменение алгоритма декомпозиции под конкретную математическую модель позволит уменьшить размерность таблиц, но пока такого алгоритма не существует.
В связи с этим в качестве методов решения были выбраны описанные в [2] модификации симплекс-метода для случая задачи целочисленного линейного программирования. В общем случае количество операций симплекс-метода не допускает полиномиальной оценки (был даже показан класс задач, для которых количество операций составляет O(en)), но для случая нашей задачи среднее число операций допускает полиномиальную оценку: O(n3m1/(n-1)) (n – количество переменных; m – количество ограничений).
2.2.1. ????????? ????????????? ????????Этот алгоритм назван полностью целочисленным, потому что если исходная таблица состоит из целочисленных элементов, то все таблицы, получающиеся в процессе работы алгоритма, содержат только целочисленные элементы. Подобно двойственному симплекс-методу, алгоритм начинает работать с двойственно допустимой таблицы. Если ai0 (i = 1 ,…, n+m; ai0 – коэффициенты целевой функции) – неотрицательные целые, то задача решена. Если для какой-нибудь строки ai0<0, то составляется новое уравнение и записывается внизу таблицы. После этого используется двойственный симплекс-метод. Все элементы дополнительной строки должны быть целыми числами, а ведущий элемент равен –1. Введенная таким образом ведущая строка сохранит таблицу целочисленной.
Пусть задана задача целочисленного линейного программирования:
максимизировать

при условиях
![]()
![]()
|
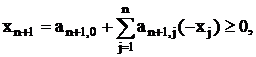
![]()
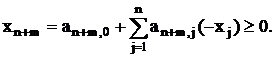
Условия (12) могут быть записаны как
|
![]()
Предположим, что для t=0 (т.е. для исходной таблицы) все aij – целые и столбцы ![]() (j = 1 ,…, n) – лексикографически положительны. Тогда все столбцы на протяжении вычислений остаются лексикографически положительными.
(j = 1 ,…, n) – лексикографически положительны. Тогда все столбцы на протяжении вычислений остаются лексикографически положительными.
Прежде чем изложить способ получения дополнительного ограничения из производящей строки, введем новое представление чисел. Пусть [x] обозначает наибольшее целое число, не превосходящее x. Для любого числа y (положительного или отрицательного) и положительного ![]() можно записать:
можно записать:
|
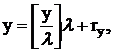
где ![]() (ry – неотрицательный остаток от деления нацело y на
(ry – неотрицательный остаток от деления нацело y на ![]() ). В частности,
). В частности, ![]() . Поэтому если
. Поэтому если ![]() , то
, то ![]() и r = 1. Если
и r = 1. Если ![]() , то
, то ![]() и r = 0.
и r = 0.
Вводимое дополнительное неравенство должно выполняться при любом целом решении задачи (12). Рассмотрим некоторое уравнение в t – таблице (опуская индекс строки) с a0<0:
|