Дипломная работа: Разработка программно–алгоритмических средств для определения надёжности программного обеспечения на основании моделирования работы системы типа "клиент–сервер"

Регистрация, сбор и анализ характеристик ошибок в программах является сложным и трудоемким процессом. Поэтому имеется относительно небольшое число работ, в которых опубликованы реальные характеристики ошибок.

При автономной, и в начале комплексной отладки доля системных ошибок невелика (~ 10%), но она существенно возрастает (до 35–40%) на завершающих этапах комплексной отладки. В процессе сопровождения системные ошибки являются преобладающими (~ 80% от всех ошибок).

Различными авторами были сделаны ряд уточнений вышеизложенной модели (к настоящему времени предложено около 15 математических моделей для описания количества ошибок в ПО различной степени сложности). Однако ни одна из этих моделей не имеет явных преимуществ по точности аппроксимации распределений и прогнозирования числа ошибок в программах по сравнению с простейшей экспоненциальной моделью. Обзор наиболее характерных моделей надежности ПО дается в Приложении А.

В работе [20] дается сравнение моделей. Модели Джелинского–Моранды и Шика–Уолвертона целесообразны при моделировании надежности ПО небольшого объема, а модифицированная модель Шика–Уолвертона – для ПО больших проектов. Если при моделировании необходимо получить значения надежности (например, среднюю наработку до отказа), то лучше использовать геометрические модели. Некоторые модели не имеют решений (то есть расходятся при определенных входных условиях). Если имеются данные об интервалах времени между ошибками, то лучше воспользоваться геометрической моделью, а если имеются данные о числе ошибок, приходящихся на единицу времени, то лучше применять модель Шнейдевинда. Экспоненциальная и дискретная модели были проверены при тестировании реальных программ и хорошо соответствуют действительности [21].

В заключение в [20] делается вывод, что на сегодняшний день невозможно выбрать наилучшую модель среди десятка предложенных.

Из–за значительных неопределенностей во всех вышеописанных моделях в [11] рекомендуется использовать несколько моделей одновременно и объединять их результаты.

В [19] говорится, что модели дают удовлетворительный результат при относительно высоких уровнях интенсивности проявления ошибок, то есть при невысокой надежности ПО. В этих условиях математические модели предназначены для приближенной оценки:

потенциально возможной надежности функционирования программ в процессе испытаний и эксплуатации;

числа пропущенных ошибок;

время тестирования, требуемое для обнаружения следующей ошибки;

время, необходимое для обнаружения с заданной вероятностью большинства имеющихся ошибок.

Можно предположить, что оценки, приведенные для нескольких конкретных систем, позволят прогнозировать эти характеристики для других проектов. Вероятностный подход к надежности ПО должен дать ответ на один из самых сложных вопросов при тестировании ПО – когда нужно остановиться и завершить тестирование, то есть, в течении какого времени времени нужно тестировать программу, чтобы она удовлетворяла требованиям по надежности? С помощью предложенной в данной работе модели надежности можно получить ответ на этот вопрос.

2.2 Содержательная постановка задачи

Имеется ПО типа "клиент–сервер". Сервер обслуживает запросы от N программ–клиентов (далее просто клиенты, рис.7). В ПО равномерно по области определения входных данных (ООД) (A, B) расположены Er ошибок.

Ошибками (отказами) ПО являются:

Отказы в программе. Если ПО не модифицируется, то интенсивность его отказов остаётся постоянной.

Внутренние отказы в программе. Такие отказы обусловлены фундаментальными ограничениями алгоритма, используемого в ПО (например, использование эвристических алгоритмов может привести к случайным отказам).

Отказы, обусловленные ограничением на функционирование в реальном времени. В рассматриваемых системах среда может изменяться динамически. Поэтому если планирования или расчёта отклика слишком велико, то к моменту выполнения отклика среда может быть уже изменена настолько, что вычисленный или спланированный отклик не будет иметь требуемого эффекта.

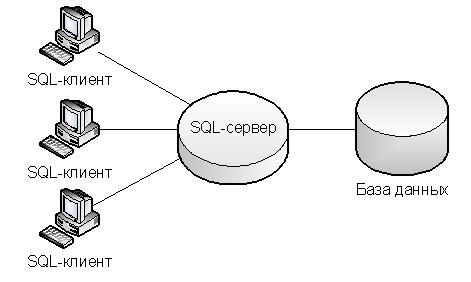
Рисунок 7 – Типовая клиент-серверная структура

Сервер сложнее программ–клиентов с точки зрения разработки ПО в S раз. S – коэффициент сложности сервера по отношению к клиентам. Каждый k–ый (k = 1, 2, …, N) клиент порождает пуассоновский поток данных к серверу интенсивностью lобр. Данные от клиента распределены по ООД по нормальному закону с характеристиками mk и sk, где mk распределено между клиентами равномерно по всей области входных данных, 3sk – распределено равномерно на меньшем из участков отсекаемых mk на оси области данных. Это нужно для имитации неравномерности использования ООД при малом количестве клиентов.

На запрос клиента сервер отвечает данными, которые распределены равномерно по всей области определения данных (A, B).

На рис. 8 изображено распределение запросов одного клиента по области всех возможных запросов к серверу, а также показано равномерное расп