Дипломная работа: Рентгеноструктурний аналіз молибдену

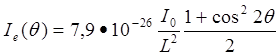(22)

Отже, один вільний електрон розсіює в одиницю тілесного кута 10^-26 частину інтенсивності первинного пучка. Це значення розсіюваної інтенсивності приймають за умовну одиницю і використовують для нормування кривих інтенсивності. Приведені формули справедливі для будь-якого електромагнітного випромінювання, у тому числі і для видимого світла, довжини хвиль якого набагато більше розміри атомів і молекул.

Проте у разі видимого світла хвилі, випромінювані атомами і молекулами, не інтерферують одна з одною, оскільки під дією світлової хвилі всі електрони атомів здійснюють коливання в однаковій фазі. Атоми і молекули в полі світлової хвилі поводяться подібно елементарним електричним диполям. Картина істотно змінюється, якщо довжина хвилі падаючого випромінювання менше розміру атома. Тепер уже електрони в різних частинах атома коливаються в неоднакових фазах. Випромінювані ними хвилі приходять в точку спостереження з деякою різницею фаз і інтерферують одна з одною. Результат цієї інтерференції залежить від числа електронів в атомі і їх просторового розподілу. Досвід показує, що не все розсіяне випромінювання має ту ж довжину хвилі, що і первинне. Деяка його частина розсівається атомами некогерентно і участі в інтерференції не бере. У структурному аналізі використовується тільки когерентне розсіювання.

Розсіювання рентгенівського випромінювання вільним атомом

Електрони в атомі не можна розглядати як вільні, тому інтенсивність розсіювання рентгенівського випромінювання атомом не може бути одержана простим складанням інтенсивностейрозсіювання окремими електронами. При розрахунку інтенсивності розсіювання атомом необхідно враховувати різницю фаз вторинних хвиль, випромінюваних електронами в різних точках атома.

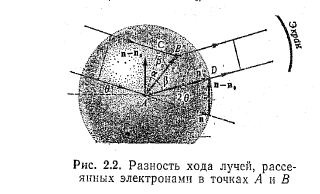
Розглянемо спочатку два електрони, що знаходяться в атомі в точках А і B на відстані r один від одного. Позначимо nіn₀ — одиничні вектори у напрямі нормалі до фронту падаючої і розсіяної хвилі (мал. 2.2). Різниця ходу проміння, розсіяного електронами,

∆l = |AD|—|CB| = rcosβ—rcosβ₀ = rn —rn ₀ = r (n —n ₀ ) (23)

де β₀ —кут між напрямом падаючого променя і вектором r ; β—те ж, для розсіяного променя. Якщо r (n —n ₀ ) = 2k(λ/2) те розсіяні хвилі підсилять одна одну, якщо ж r (n —n ₀ ) = (2k + 1) λ/2 те ослаблять. Рівняння (23) виражає умову інтерференції розсіяних хвиль

r(cosβ—cosβ₀ ) = kλ(24)

При k = 1 і β₀ = 90° одержуємо cos β =λ/r . Оскільки cosβ ≤ l, то звідси витікає, що інтерференція розсіяних хвиль виникає лише у разі, коли довжина хвилі менше відстані між частинками, що розсіюються. Якщо ж λ > r, інтерференція розсіяних хвиль не відбувається, Помноживши (23) на хвильове число 2π/ λ, одержимо вираз для різниці фаз хвиль, розсіяних двома електронами атома,

∆φ = (2π/ λ)r (n —n ₀ ) (25)

Припустимо, що електрони в атомі розподілені безперервно. Виділимо в ньому елемент об'єму dV_i і позначимо ρ_e (r_i ) — електронну густину в точці на відстані r_i від центру атома. Тоді число електронів, що знаходяться в об'ємі dV_i визначиться величиною ρ_e (r_i ) dV_i а амплітуда хвилі, розсіяної ними, — добутком

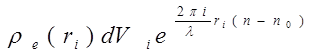
Сумарна амплітуда хвиль, розсіяних атомом,

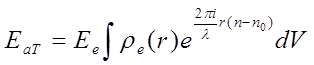(26)

Вектор n —n ₀ співпадає з напрямом нормалі до площини, що відображає рентгенівське випромінювання. У атомі відбиваючих площин зрозуміло ні. Проте поняттям «нормаль до відбиваючої площини», ми користуватимемося і в даному випадку, оскільки вектор n —n ₀ визначає напрям осі, від якої відлічується полярний кут.

Якщо кут між напрямами первинного пучка і уявною площиною, що відображає, позначити θ, то кут розсіювання 2θ. Очевидно, що |n —n ₀ | = 2sinθ(мал.2.2) Позначаючи α — кут між векторами r і n —n ₀ , одержимо для різниці фаз розсіяних хвиль вираз

(27)

де S = (4π/λ)sinθ Параметр S, залежний від довжини хвилі і кута розсіювання, зустрічається в структурному аналізі і в теорії твердого тіла. Він пов'язаний з міжплощинною відстанню d для площин кристалічних граток, від яких походить віддзеркалення першого порядку під кутом θпри довжині хвилі λ.Згідно умові віддзеркалення 2dsinθ= λ , маємо

2sinθ/ λ = 1/d або 4πsinθ/ λ = 2π/d, тобто S = 2π/d(28)

З другого боку, параметр S пов'язаний з хвильовим вектором розсіяної хвилі співвідношенням

S = 2|k |sinθ(29)

а також з вектором оберненої гратки рівністю

S = 2π|r * | (30)

Підставляючи (27) в (26), одержимо для амплітуди розсіювання атомом вираз

(31)

Щоб додати йому конкретніший вигляд, припустимо, що розподіл електронів в атомі сферично симетричний і ρ(r) залежить тільки від модуля вектора r , але не від його напряму. В цьому випадку елемент об'єму dV = r² drsinαdαdφ. Вираз (31) можна написати у вигляді

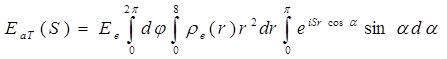(32)

Інтегруючи (32) по α і φ, одержимо