- аутентифікація сторін, що встановлюють зв'язок;

- авторизація користувачів при доступі до телекомунікаційних і інформаційних служб.

Окрім перерахованих вище класичних областей застосування протоколів існує широкий круг специфічних завдань, що також вирішуються за допомогою відповідних криптографічних протоколів. Це перш за все розкриття частини відомостей без обнародування самого секрету в його справжньому об'ємі, а також часткове розкриття секрету.

Метою даної роботи є системний аналіз роботи криптографічних протоколів і створення математичних імовірнісних моделей елементів криптографічних систем з метою формалізації оцінок стійкості криптопротоколів.

Для досягнення мети необхідно вирішити наступні завдання:

1. Аналіз структури захищених систем, що використовують криптографічні протоколи.

2. Системний аналіз методик оцінки стійкості шифрів і протоколів.

3. Розробка пропозицій по формалізації завдання оцінки стійкості протоколів, заснованої на імовірнісних моделях.

Актуальність проблеми полягає в тому, що в сучасних умовах велика кількість завдань забезпечення інформаційної безпеки різних систем ефективно розв'язується за допомогою криптографічних протоколів, що обумовлює і посилення роботи криптоаналітиків по реалізації всіляких атак на протоколи. Це викликає необхідність підвищення надійності і безпеки роботи протоколів. Для ефективної протидії погрозам доцільно розробити імовірнісну модель криптопротоколів, стійку до модельованих атак на них, тобто формалізувати доказ стійкості.

Розділ 1. Структура захищених систем і їх характеристики

1.1. Структура захищеної системи обміну даними

Щоб приступити до математичного аналізу криптосистем необхідно показати структуру захищеної системи обміну даними, яка представлена на мал.1.1.

Шифрувальник

повідомлення

	Джерело повідомлень	Шифруваль ник TK	Шифврувальник TK

Повідомлення Криптограма Повідомлення

Ключ К Ключ К

Джерело ключів

Мал. 1.1

На передавальному кінці є два джерела інформації – джерело повідомлення і джерело ключів. Джерело ключів відбирає конкретний ключ серед всіх можливих ключів даної системи. Цей ключ передається деяким способом на приймальний кінець, причому передбачається, що його не можна перехопити (наприклад, ключ передається посильним). Джерело повідомлень формує деяке повідомлення (незашифроване), яке потім зашифровується, і готова криптограма передається на приймальний кінець, причому криптограма може бути перехоплена. На приймальному кінці шифрувальник за допомогою ключа по криптограмі відновлює початкове повідомлення.

Очевидно, шифрувальник на передавальному кінці виконує деяку функціональну операцію. Якщо М – повідомлення, К – ключ і Е – зашифроване повідомлення, то маємо

Е= ¦ (М, К )

тобто Е є функцією від М і К . Зручніше, проте, розуміти Е не як функцію двох змінних, а як (однопараметричне) сімейство операцій або відображень і записувати його у вигляді:

Е = Т_i М.

Відображення Т_i , застосоване до повідомлення М , дає криптограму Е. Індекс i відповідає конкретному використовуваному ключу.

Взагалі ми припускатимемо, що є лише кінцеве число можливих ключів, кожному з яких відповідає вірогідність р _i . Таким чином, джерело ключів є статистичним процесом, або пристроєм, який вибирає одне з множини відображень Т ₁ , …, Т _m з імовірністю р ₁ , …, р _m відповідно. Також припускатимемо, що число можливих повідомлень скінчене, і ці повідомлення М ₁ , …, М _n мають апріорну імовірність q ₁ , …, q _n . Наприклад, можливими повідомленнями могли б бути всілякі послідовності англійських букв, що включають по N букв кожна, а відповідною імовірністю тоді були б відносні частоти появи таких послідовностей в нормативній англійській мові.

Повинна бути можливість відновлювати М на приймальному кінці, коли відомі Е і К . Тому відображення Т_i з нашого сімейства повинна мати єдине зворотне відображення Т_i ^{- 1} , так що Т_i Т_i ^{- 1} =I , де I – тотожнє відображення. Таким чином, це зворотне відображення Т_i ^{- 1} повинне існувати і бути єдиним для кожного Е, яке може бути одержане з М за допомогою ключа i.

1.2. Сучасні основні шифри

За характером використання ключа відомі кріптосистеми можна розподілити на два типи: симетричні (одноключові, з секретним ключем) і несиметричні (з відкритим ключем).

У першому випадку в шифраторі відправника і дешифраторі одержувача використовується один і той же ключ. Шифратор утворює шифртекст, який є функцією відкритого тексту, конкретний вид функції шифрування визначається секретним ключем. Дешифратор одержувача повідомлення виконує зворотне перетворення аналогічним чином. Секретний ключ зберігається в таємниці і передається відправником повідомлення одержувачу по каналу, що виключає перехоплення ключа криптоаналітиком супротивника.

Як приклад симетричного алгоритму шифрування розглянемо достатньо стійкий і надійний алгоритм DES (Data Encryption Standard).

У криптосистемах з відкритим ключем в алгоритмах шифрування і дешифрування використовуються різні ключі, кожний з яких не може бути одержаний з іншого (з прийнятними витратами). Один ключ використовується для шифрування, інший – для дешифрування. Основний принцип систем з відкритим ключем грунтується на застосуванні односторонніх або необоротних функцій і односторонніх функцій з лазівкою («потайним ходом»). Обчислення ключів здійснюється одержувачем повідомлень, який залишає у себе той ключ, який він потім використовуватиме (тобто секретний ключ). Інший ключ він висилає відправнику повідомлень – відкритий ключ – не побоюючись його розголосу. Користуючись цим відкритим ключем, будь-який абонент може зашифрувати текст і послати його одержувачу, який згенерував даний відкритий ключ. Всі використовувані алгоритми загальнодоступні. Важливо те, що функції шифрування і дешифрування оборотні лише тоді, коли вони забезпечуються строго взаємозв'язаною парою ключів (відкритого і секретного), а відкритий ключ повинен бути необоротною функцією від секретного ключа. Так само шифртекст повинен бути необоротною функцією відкритого тексту, що в корені відрізняється від шифрування в системах з секретним ключем.

Як алгоритм з відкритим ключем далі розглянемо один з найбільш поширених шифр RSA (Rivest - Shamir - Adleman). Його надійність знаходиться в прямій залежності від складності розкладання великих чисел на множники. Якщо множники мають довжину близько 100 десяткових цифр, то в найкращому з відомих способів розкладання на множники необхідно близько 100 млн. років машинного часу, шифрування ж і дешифрування вимагає близько 1-2 с на блок.

Опис алгоритму DES.

У криптосистемі DES використовується блоковий принцип шифрування двійкового тексту. Довжина блоку шифрування складає 64 біта. Розмір ключа - також 64 біта. При цьому кожен восьмий біт є службовим і в шифруванні не бере участь. Кожен такий біт є двійковою сумою семи попередніх і служить лише для виявлення помилок при передачі ключа по каналу зв'язку. Процес криптоперетворення містить наступні три основні етапи.

1. Біти початкового повідомлення x піддаються початковій підстановці IP відповідно до табл. 1.1.

Таблиця 1.1

Підстановка IP

58	50	42	34	26	18	10	2	60	52	44	36	28	20	12	4
62	54	46	38	30	22	14	6	64	56	48	40	32	24	16	8
57	49	41	33	25	17	9	1	59	51	43	35	27	19	11	3
61	53	45	37	29	21	13	5	63	55	47	39	31	23	15	7

Це означає, що 58-й біт стає першими, 50-й - другим і т.д. Потім одержаний вектор x₀ = IP(x) представляється у вигляді x₀ =L₀ R₀ , де L₀ – ліва половина з 32 бітів, а R₀ – права половина з 32 бітів.

2. Повідомлення L₀ R₀ перетворюється далі 16 разів по так званій схемі Фейстеля:

L_i =R_{i- 1} , R_i = L_{i- 1} Å ¦( R_{i- 1} , K_i ), i = 1, 2, …, 16,

де функція ¦ і розклад ключів K ₁ , K ₂ , …, K ₁₆ будуть описані окремо.

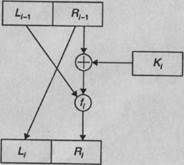
Мал. 1.2 Криптоперетворення Фейстеля