Дипломная работа: Система стиснення відеоданих на основі аналізу ентропійності

У цьому випадку r_i ^{(sj) -} емпірична оцінка ймовірності появи символу з індексом i при породженні j-й вибірки джерела інформації¹ . Причина, по якій особлива увага приділяється способах обчислення ентропії, полягає в тім, що величина ентропії є чисельною границею ефективності ощадливого кодування вибірки інформаційного джерела. Знаючи ентропію, можна оцінити ефективність того або іншого методу або алгоритму. В ідеалі ефективність винна збігатися з величиною ентропією. При цьому, якщо природа інформаційного джерела не є імовірнісної, тобто чітко виділити ті або інші імовірнісні стани не можна, мова може йти тільки про ентропію, що обчислює частково на емпіричній основі. В силу останньої обставини, надалі при вживанні терміна ентропія найчастіше буде матися на увазі напівемпірична ентропія.

Обчислення ентропії на практиці можна здійснювати в процесі послідовного аналізу станів інформаційного джерела, що безпосередньо треба з формул (1.5) і (1.6). Як видно з наведених формул, величина ентропії складається з величин ентропії в станах, у яких послідовно перебуває джерело інформації. Таким чином, задача оптимального моделювання послідовної інформаційної вибірки зводиться до задачі створення оптимальної моделі породження символів у шкірному конкретному стані, що є істотним спрощенням. Як буде показаний нижче, подібне спрощення припустиме й відносно механізму генерації коду, тобто воно фактично припустимо відносно методу кодування в цілому.

1.2.2 Дешифровані коди

Найпростіший варіант кодування вибірки інформаційного джерела - установлення відповідності між конкретними символами алфавіту й кодами, що мають цілу довжину в одиницях подання інформації. Природно зажадати, щоб код, отриманий у результаті такого кодування, був дешифрованим, тобто по будь-якій комбінації кодів символів можна було б відновити закодоване повідомлення. Необхідна умова дешифруємості було запропоновано й доведене Макмілланом. Формулювання виглядає в такий спосіб: якщо система кодів із цілими довжинами {li}^N _i =1 дешифровані, те виконується нерівність

(1.7)

де m - підстава системи подання інформації.

Виконання нерівності (1.7) спричиняє виконання більше важливої нерівності:

(1.8)

Для доказу досить скористатися опуклістю функції log_m (x ). Таким чином, ефективність дешифрованого посимвольного кодування обмежена величиною ентропії імовірнісного розподілу появи символів на виході інформаційного джерела.

Більше складний й у той же час найбільше ефективний варіант кодування має на увазі одержання кодів не для окремих символів, а для цілих повідомлень. Коди декодуємих повідомлень, мабуть, також повинні задовольняти нерівності Макміллана. При цьому оцінка ефективності з розрахунку на один символ повідомлення ускладнюється необхідністю проведення усереднення по довжині повідомлення. Покажемо, що ефективність кодування вибірки інформаційного джерела зазначеним способом також обмежується величиною ентропії.

Будемо використати раніше уведені позначення. Джерело, що послідовно перебуває в станах s 1, s 2,..., s_n , як і раніше, характеризується імовірнісними розподілами

.

Через p_{i 1, i 2,..., in} позначається ймовірність появи повідомлення "i 1, i2,... i_n ", через l_{i 1, i 2,..., in} - довжина коду повідомлення. Ефективність кодування повідомлень довжини n з розрахунку на один символ визначається по формулі

Коди для повідомлень довжини n повинні бути дешифрованими, тому можна скористатися нерівністю (1.8):

Права частина нерівності являє собою вираження для ентропії. Таким чином, ефективність кодування з розрахунку на один символ не може перевершувати величину ентропії повідомлення, що доводити на один символ. Використовуючи формулу (1.5), одержуємо більше зручну з обчислювальної крапки зору оцінку:

Якщо джерело, що породжує повідомлення, є стаціонарним (імовірнісний розподіл не залежить від позиції символу в повідомленні), нерівність здобуває спрощений вид:

1.2.3 Оптимальна довжина коду

Тому що код виходить для повідомлення в цілому, не можна говорити про коди для конкретних символів, що становлять повідомлення. Проте виникає необхідність визначати деякий внесок у результуючу довжину коду повідомлення, внесень кожним вхідної в нього символом. Фізичний зміст такого внеску - середнє збільшення довжини коду повідомлення, обумовлене входженням у нього даного символу. Позначимо через x_i внесок, внесень символом з індексом i ( у загальному випадку величина внеску являє собою речовинне число). Через x_{i 1, i 2,..., in} позначимо внесок, внесень повідомленням s = i₁ , i₂ ,..., i_n - Виходячи зі змісту поняття "внесок", для випадку стаціонарної незалежної вибірки логічно зажадати виконання наступних властивостей:

₍ адитивність)

,

де l_{i 1, i2,..., in} - довжина реального коду повідомлення (ціле число), а M (n) - ненегативна функція, така що M (n) /n - > 0 при n - > оо

Асимптотичне поводження функції M (n) /n дозволяє зробити висновок:

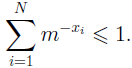(1.9)

Таким чином, отримане узагальнення нерівності Макміллана на випадок внесків символів у результуючу довжину повідомлень.

Узагальнена нерівність (1.9) дозволяє обчислити точне значення величини внеску x_a символу з індексом a для випадку оптимального кодування. Для обчислення точного значення необхідно вирішити задачу про мінімізацію суми

,

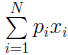яка визначає середню ефективність кодування, за умови виконання нерівності (1.9). У крапці мінімуму похідна від зазначеної суми звертається в нуль:

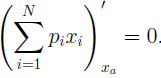(1.10)

Підстановка рішення задачі про мінімізацію в нерівність (1.9), мабуть, повинне перетворювати його в рівність. Звідси будь-який оптимальний внесок x_k легко виражається через внески інших символів:

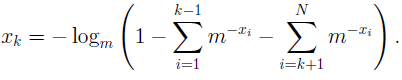
Підставляючи вираження для x_k у рівняння (1.10), одержуємо