Дипломная работа: Структурная надежность систем
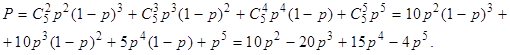(3.19)
Вероятность отказа той же системы по (3.17):
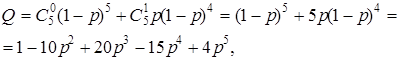(3.20)
что, как видно, дает тот же результат для вероятности безотказной работы.
В табл. 3.2 приведены формулы для расчета вероятности безотказной работы систем типа “m из n“ при m<=n<=5. Очевидно, при m=1 система превращается в обычную систему с параллельным соединением элементов, а при m = n - с последовательным соединением.
Таблица 3.2
| Общее число элементов , n | |||||
| m | 1 | 2 | 3 | 4 | 5 |
| 1 |  |  |  |  |  |
| 2 | - |  |  |  |  |
| 3 | - | - |  |  |  |
| 4 | - | - | - |  |  |
| 5 | - | - | - | - |  |
3.4. Мостиковые схемы
Мостиковая структура (рис. 3.2, а, б) не сводится к параллельному или последовательному типу соединения элементов, а представляет собой параллельное соединение последовательных цепочек элементов с диагональными элементами, включенными между узлами различных параллельных ветвей (элемент 3 на рис. 3.2, а, элементы 3 и 6 на рис. 3.2, б). Работоспособность такой системы определяется не только количеством отказавших элементов, но и их положением в структурной схеме. Например, работоспособность ТС, схема которой приведена на рис. 3.2, а, будет утрачена при одновременном отказе элементов 1 и 2, или 4 и 5, или 2, 3 и 4 и т.д.. В то же время отказ элементов 1 и 5, или 2 и 4, или 1, 3 и 4, или 2, 3 и 5 к отказу системы не приводит.
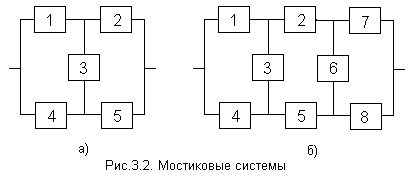
Таблица 3.3
Таблица состояний мостиковой системы
 | Состояние элементов | Состояние | Вероятность состояния | |||||
| сост. | 1 | 2 | 3 | 4 | 5 | системы | в общем случае | при равнонадежных элементах |
| 1 | + | + | + | + | + | + |  | |
| 2 | + | + | + | + | - | + |  |  |
| 3 | + | + | + | - | + | + |  | |
| 4 | + | + | - | + | + | + |  | |
| 5 | + | - | + | + | + | + |  | |
| 6 | - | + | + | + | + | + |  | |
| 7 | + | + | + | - | - | - |  |  |
| 8 | + | + | - | + | - | + |  | |
| 9 | + | - | + | + | - | + |  | |
| 10 | - | + | + | + | - | + |  | |
| 11 | + | + | - | - | + | + |  | |
| 12 | + | - | + | - | + | + |  | |
| 13 | - | + | + | - | + | + |  | |
| 14 | + | - | - | + | + | + |  | |
| 15 | - | + | - | + | + | + |  | |
| 16 | - | - | + | + | + | - |  | |
| 17 | + | + | - | - | - | - |  |  |
| 18 | + | - | + | - | - | - |  | |
| 19 | - | + | + | - | - | - |  | |
| 20 | + | - | - | - | + | - |  | |
| 21 | - | + | - | - | + | + |  | |
| 22 | - | - | - | + | + | - |  | |
| 23 | + | - | - | + | - | + | | |
| 24 | - | + | - | + | - | - |  | |
| 25 | - | - | + | - | + | - |  | |
| 26 | - | - | + | + | - | - |  | |
| 27 | + | - | - | - | - | - |  |  |
| 28 | - | + | - | - | - | - |  | |
| 29 | - | - | + | - | - | - |  | |
| 30 | - | - | - | + | - | - |  | |
| 31 | - | - | - | - | + | - |  | |
| 32 | - | - | - | - | - | - |  |  |
Для расчета надежности мостиковых систем можно воспользоваться методом прямого перебора , как это было сделано для систем “m из n“ (п. 3.3), но при анализе работоспособности каждого состояния системы необходимо учитывать не только число отказавших элементов, но и их положение в схеме (табл. 3.3). Вероятность безотказной работы системы определяется как сумма вероятностей всех работоспособных состояний:
(3.21)
В случае равнонадёжных элементов
(3.22)
Метод прямого перебора эффективен только при малом количестве элементов n , о чем говорилось в начале разд. 3, поскольку число состояний системы составляет 
. Например, для схемы на рис. 3.2,б их количество составит уже 256. Некоторое упрощение достигается, если в таблицу состояний включать только сочетания, отвечающие работоспособному (или только неработоспособному) состоянию системы в целом.
Для анализа надежности ТС, структурные схемы которых не сводятся к параллельному или последовательному типу, можно воспользоваться также методом логических схем с применением алгебры логики (булевой алгебры). Применение этого метода сводится к составлению для ТС формулы алгебры логики, которая определяет условие работоспособности системы. При этом для каждого элемента и системы в целом рассматриваются два противоположных события - отказ и сохранение работоспособности.
Для составления логической схемы можно воспользоваться двумя методами - минимальных путей и минимальных сечений.
Рассмотрим метод минимальных путей для расчета вероятности безотказной работы на примере мостиковой схемы (рис. 3.2,а).
Минимальным путем называется последовательный набор работоспо-собных элементов системы, который обеспечивает ее работоспособность, а отказ любого из них приводит к ее отказу.
Минимальных путей в системе может быть один или несколько. Очевидно, система с последовательным соединением элементов (рис. 2.1) имеет только один минимальный путь, включающий все элементы. В системе с параллельным соединением (рис. 2.2) число минимальных путей совпадает с числом элементов и каждый путь включает один из них.
Для мостиковой системы из пяти элементов (рис. 3.2,а) минимальных путей четыре: (элементы 1 и 4), (2 и 5), (1, 3 и 5), (2, 3 и 5). Логическая схема такой системы (рис. 3.3) составляется таким образом, чтобы все элементы каждого минимального пути были соединены друг с другом последовательно, а все минимальные пути параллельно.
Затем для логической схемы составляется функция алгебры логики А по общим правилам расчета вероятности безотказной работы , но в