Дипломная работа: Теория вероятности и математическая статистика

, которая называется 1 бит.

Неопределенность исхода испытания до испытания автоматически определяет информативность исхода испытания после испытания. Поэтому в битах также измеряется информативность исхода.

Рассмотрим два вероятностных пространства:

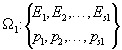
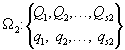
Проводим композицию двух испытаний. Композиционное пространство имеет вид:

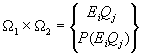i=1, ..., s1 j=1, ..., s2

С точки зрения качественного анализа максимальная энтропия композиционного вероятностного пространства достигается тогда, когда испытания независимы. Найдем энтропию композиционного пространства для случая независимых испытаний.

Биномиальное распределение.

n испытаний называются системой испытаний Бернулли, если испытания независимы, в каждом из них происходит событие , либо с вероятностью наступления P(A) = p;

Найдем вероятность того, что в результате проведенных n испытаний событие А произошло m раз:

Рассмотрим композицию n независимых испытаний и построим композиционное пространство элементарных событий.

Общий вид элемента этого пространства следующий:

где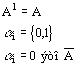

При этом вероятность наступления такого события равна:

(умножение при независимых событиях)

Найдем вероятность наступления любого элементарного события из композиционного пространства:

Рассмотрим в композиционном вероятностном пространстве событие: в n испытаниях событие A произошло m раз.

Событие A состоит из - общее кол-во элементарных событий, в которое входит событие А. А произошло m раз, - n-m раз. Вероятность каждого из этих элементарных событий одинакова и равна:

Следовательно, на основании III аксиомы теории вероятности результат равняется:

(сложение вероятностей)

Случайная величина

Пусть имеется вероятностное пространство вида .

Случайной величиной называется измеримая числовая скалярная функция , элементами которой являются элементарные события.