Доклад: Эксплуатационные свойства машин и механизмов

Рис. 2.3. Схемы плоских механизмов
Кривошипом (поз. 1 на рис. 2.3) называется звено, соединенное со стойкой вращательной парой и совершающее относительно стойки полное вращательное движение. Коромысло (поз. 3 на рис. 2.3, а) также соединено со стойкой вращательной парой, но совершает относительно нее неполное вращательное (качательное) движение. Кулисой (поз. 3 на рис. 2.3, в, г) называется звено с подвижными направляющими, соединенное со стойкой вращательной или поступательной парой. Ползун (поз. 3 на рис. 2.3, б) соединен со стойкой поступательной парой и совершает поступательное движение. Звено (поз. 2 на рис. 2.3, а, б), совершающее относительно стойки плоское (совокупность поступательного и вращательного) движение и соединенное с другими звеньями вращательными парами, называется шатуном.
В кулисном механизме (рис. 2.3, в) звенья 2 и 3 могут иметь разное конструктивное оформление. Звено 2 совершает поступательное движение в направляющих кулисы и называется кулисным камнем.
Под степенью подвижности механизма понимается число независимых параметров, которое необходимо задать для определения положения всех подвижных звеньев. Грубо говоря, это число двигателей, необходимое для получения на выходе механизма определенного движения (каждый двигатель – одна координата, параметр). В механизме с одной степенью подвижности достаточно задаться значением одного параметра для определения положения всех подвижных звеньев Преимущественное распространение получили механизмы с одной и двумя (дифференциальный зубчатый механизм) степенями подвижности.
При аналитическом определении степени подвижности составляется система сложных нелинейных уравнений связи между параметрами относительного движения.
Практически степень подвижности механизма определяется из его структурной формулы, связывающей степень подвижности с числом звеньев механизма, числом и видом кинематических пар. Для пространственного механизма структурная формула определяется выражением
w = 6 ´ (n - 1) – 5 ´p5 – 4 ´p4 – 3 ´p3 –2 ´p2 –1 ´p1 ,
где (n - 1) – число подвижных звеньев (n – общее число звеньев, включая и стойку),
pi – число кинематических пар класса i, входящих в состав механизма,
i – число связей, накладываемых парой класса i.
Для плоских механизмов при определении степени подвижности можно использовать структурную формулу Сомова и Чебышева:
w = 6 ´ (n - 1) – 5 ´p5 – 4 ´p4 .
При проектировании таких механизмов заранее предопределяется, что их звенья не могут совершать трех движений (из коэффициентов вычитается 3): вращений вокруг осей x и y и поступательного движения вдоль оси z, перпендикулярной плоскости xy (т.е. накладываются три общих для всех звеньев связи).
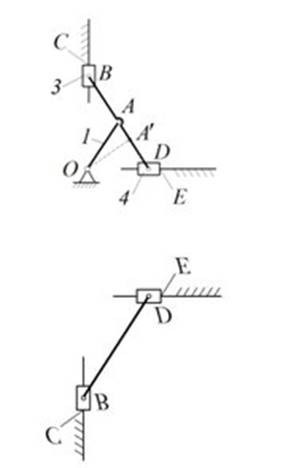
Рис. 2.4. Механизм эллипсографа
При проектировании механизмов нужно исключить возможность появления избыточных связей, при которых может возникнуть заклинивание механизма. Примером является механизм эллипсографа: произвольные точки отрезка BD описывают эллипсы, и только его середина (т. А) движется по окружности (рис. 2.4, а). Из структурной формулы (n =5, p5 = 6) следует, что w = 0. Если точку А сместить от середины отрезка, то действительно w = 0. Поэтому целесообразно изменить структуру механизма, изъяв звено ОА (и кинематические пары О и А) или один из ползунов 3 или 4 (кинематические пары, соединяющие ползун со стойкой и шатуном) (рис. 2.4, б). К избыточным связям могут приводить погрешности изготовления и сборки.
6. Анализ и синтез механизмов
В инженерной практике часто требуется решение аналитическими методами двух основных задач – анализа и синтеза, представляющих собой диалектическое единство противоположностей. Они противоположны, т.к. взаимно обратны. Единство этих задач с математической точки зрения состоит в том, что решают их, как правило, с помощью одних и тех же математических моделей и уравнений [1].
[Крайнев] Анализ механизма – исследование кинематических и динамических свойств механизма по заданной его схеме (рис. 2.5).
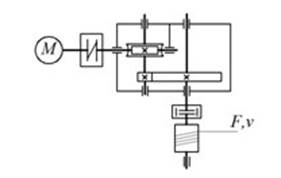
Рис. 2.5. Анализ механизма
![]()
![]() ;
; ![]() ;
;
![]() ;
;
![]()
Синтез механизма – проектирование схемы механизма по заданным его свойствам. Включает выбор структурной схемы (структурный синтез) и определение постоянных параметров выбранной схемы механизма по заданным его свойствам (параметрический синтез). Различают также кинематический и динамический синтез (Крайнев). Если предположить, что на рис. 2.6 изображено только расположение входного и выходного валов редуктора и приведены только частоты их вращения, то изображенные внутри корпуса передачи являются одним из вариантов синтеза редуктора.
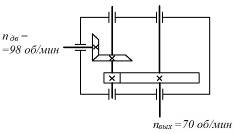
Рис. 2.6. Синтез механизма