Доклад: Идеальное - реально
5) модель функции:
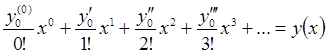
рядом Тейлора;
6) модель состояния - конструкцией (1).
Так к 1997 году выстроились первые идеальные числа Идеальной математики [5,6]. Начиная с элементарных единиц, каждое последующее идеальное число складывалось из предыдущих идеальных чисел, образуя новую конструкцию с новыми возможностями моделирования. Потому процесс абстракции идеальных чисел легко было продолжить [7]:
7) модель континуума:
- объектно-ориентированным программированием (C++, Java).
8) модель уровня:
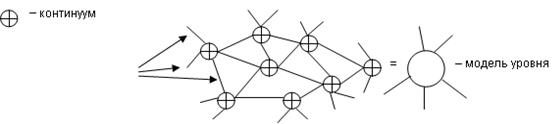
- функциональным программированием (ML, OCaml, Erlang).
9) модель развития:

![]()

 - программированием сценариев (Perl, TCL, Python, Rexx).
- программированием сценариев (Perl, TCL, Python, Rexx).
10) модель вывода

- чисто функциональным программированием (Miranda, Clean, Haskell)
Чтобы спрогнозировать дальнейшую абстракцию идеальных чисел и их операций, проанализируем путь, уже пройденный Идеальной математикой.
Ещё в 1997 году [5], исследуя градацию математических операций, найденную Идеальной математикой, отмечалось: необходимо «рассматривать не обычные числа, моделирующие неизменные постоянные количества, а переменные числа, количества которых изменяются, растут даже в период выполнения над ними той или иной операции, но не за её счёт, а сами по себе, внутри себя»; и «результат 5й ступени (модель зависимых переменных чисел) повторяет на более высоком уровне результат 1й ступени (модель независимых переменных чисел). Следовательно, и остальные операции над зависимыми переменными (6я,7я,8я ступени) подобны операциям над независимыми переменными (2я,3я,4я ступени)».
То есть, результаты простейших, самых первых операций 1й–4й ступеней (идеальные числа: натуральное, целое, рациональное, действительное) своими фундаментальными свойствами легко объединяются в отдельную группу, которую можно назвать «независимые переменные числа» или коротко – «Числа». Тогда операции в группе «Числа» назовём:
- 1я ступень: «сложение независимых переменных чисел» или коротко – «сложение чисел»;
- 2я ступень: коротко – «умножение чисел»;
- 3я ступень: коротко – «сочетание чисел»;
- 4я ступень: коротко – «возведение чисел» (размещения с повторениями).
Полученные на 4й ступени операцией «возведение чисел» «плоские» произведения, например, в работе [8] выражения (25):
![]()
Идеальной математикой преобразованы в «кружевные» произведения, например, выражения (8):
