Доклад: Идеальный газ

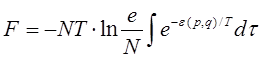
Двух- и трёхатомный газ. Вращение молекул.

Двухатомные молекулы из одинаковых атомов обладают специфическими особенностями, которые мы рассмотрим на примере пара- и ортоводорода.

Параводород

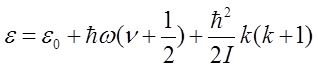
Как уже было рассмотрено, общая статсумма выражается как

“Вращательная” и “колебательная” суммы здесь определяются как

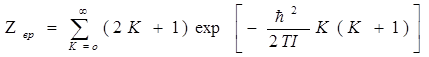
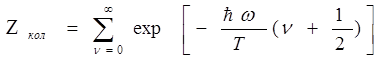
Множитель (2К+1) во вращательной сумме учитывает вырождение вращательных уровней по направлениям момента К. Свободная энергия, в конечном итоге выражается из трёх частей: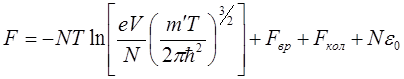

Первый член связан со степенями свободы поступательного движения молекул, назовём его поступательной частью .

Вращательная и колебательные части:

Поступательная часть всегда выражается формулой типа

, с постоянной теплоёмкостью и химической постоянной .

Полная теплоёмкость будет выражаться в виде суммы , .

Займёмся вращательной свободной энергией. Если температура настолько велика, что , то вращательная статсумма может быть заменена интегралом

Здесь e(M) – выражение кинетической энергии вращения как функции момента вращения М.

Отсюда свободная энергия

Таким образом, при рассматриваемых не слишком низких температурах вращательная часть теплоёмкости оказывается постоянной и равной в соответствии с общими результатами классического рассмотрения. Вращательная часть химической постоянной равна . Существует значительная область температур, в которой выполняется и в то же время колебательная часть свободной энергии, а вместе с нею и колебательная часть теплоёмкости отсутствуют. В этой области теплоёмкость двухатомного газа равна , т.е. , , а химическая постоянная .

В предельном случае низких температур достаточно сохранить два

первых члена суммы:

В том же приближении для свободной энергии:

Энтропия:

И, наконец, теплоёмкость:

Двухатомный газ с молекулами из

одинаковых атомов. Вращение молекул.

Двухатомные молекулы, состоящие из одинаковых атомов, обладают специфическими особенностями, что приводит к необходимости изменить полученные выше формулы.