Доклад: К столетнему юбилею Специальной теории относительности (СТО)

Реферат

Ключевые слова: Теория относительности, СТО, преобразование Лоренца, форма объекта, скорость распространения взаимодействий, причинность.

Рассмотрено изменение формы движущегося объекта и другие явления в рамках преобразования Лоренца. Показано, что интерпретация этого преобразования, предложенная А.Эйнштейном, содержит гносеологические ошибки и не может рассматриваться как научная. Предложена альтернативная интерпретация преобразования Лоренца. Ставится проблема определения границ применимости этого преобразования.

Введение

В 2005 году произойдет замечательное событие. Исполнится сто лет со дня опубликования А.Эйнштейном его Специальной теории относительности (СТО). С момента появления этой теории и до настоящего времени не прекращается критика СТО и споры относительно ее научного статуса. С одной стороны, критики неопровержимо доказывают несостоятельность СТО. С другой, апологеты СТО с не меньшим упорством защищают эту теорию, обвиняя своих оппонентов в некомпетентности. Обе стороны приводят свои аргументы. И не только аргументы. Апологеты СТО, пользуясь властью, часто используют недозволительные в науке методы: замалчивание критики, голословные обвинения в некомпетентности и т. д. Но весьма редко они выходят на "открытый бой" со своими оппонентами.

Нам хотелось бы к этому Юбилею рассмотреть явления, которым уделяется недостаточно много внимания, и ответить на следующие вопросы.

1. Имеет ли СТО внутренние противоречия, т.е. является ли она научной в правильном значении этого термина?

2. Согласуется ли СТО с результатами всех экспериментов?

3. Какова роль СТО в развитии физики?

Последнему вопросу следовало бы посвятить специальное исследование.

1. Закон "преломления" светового луча

Критики СТО ограничиваются, как правило, анализом эффектов "сокращения" масштабов движущихся тел и "замедлением" времени. К сожалению, они не принимают во внимание, что движущийся объект пролетает мимо них со скоростью v, и наблюдатель вынужден будет рассматривать этот объект под различными углами наблюдения qкак показано на рис.1

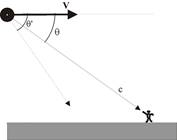
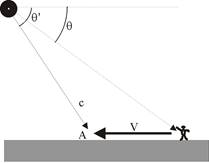
Рис 1 Рис 2

Угол qобразован двумя векторами: вектором скорости движущегося тела и вектором, направленным вдоль светового луча от движущегося источника к наблюдателю. Теоретически он может меняться от 0 до 180 градусов в системе отсчета K, связанной с наблюдателем. В системе отсчета, связанной с движущимся объектом, этот луч будет иметь другое направление, т.е. идти под другим углом. Обозначим этот угол как q'.

Причина отличия qотq' видна из рис 2. В системе K' наблюдатель и световой луч будут двигаться к общей точке встречи А. Только в этой точке наблюдатель увидит этот световой луч.

Из преобразования Лоренца известны следующие соотношения:

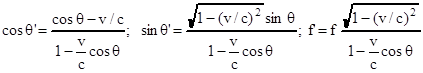
где: f и f' частоты принимаемого и излучаемого сигналов соответственно.

Запишем теперь угол расхождения между лучами (угол аберрации), который нам понадобится в дальнейшем:

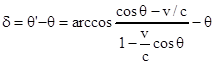
Допустим, что движущийся объект это линейка длиной Dx', ориентированная вдоль вектора скорости v. Нетрудно видеть, что наблюдаемая длина линейки будет зависеть от v и q. Кажущаяся длина линейки:

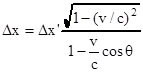
Из этого выражения следует, что известное "сокращение" масштаба

мы получаем, когда q^o . При всех других углах мы будем измерять другие значения "длин" линейки, лежащие в пределах

.

Другими словами, в общем случае измеряемая длина может быть как больше, так и меньше истинной длины линейки.

Формула, связывающая Dx и Dx', позволяет получить очень важное соотношение, которое можно назвать законом "преломления" в СТО. Для этой цели, следуя работе [1], умножим Dx на sinq и преобразуем это произведение.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--