Доклад: К столетнему юбилею Специальной теории относительности (СТО)

а) Эйнштейновский (= птолемеевский) подход. Замедление времени, которое мы наблюдаем (явление), есть "действительное" замедление времени. Время в движущейся системе отсчета действительно течет медленнее, чем в неподвижной (сущность).

б) Материалистический (= коперниканский) подход. Замедление времени есть объективное явление, которое мы наблюдаем и регистрируем в нашей инерциальной системе. Однако в самой движущейся системе время течет в том же темпе (сущность), что и в неподвижной. Кажущееся замедление времени обусловлено свойствами преобразования Лоренца (эффект Допплера).

Итак, все параметры и характеристики, полученные с помощью преобразования Лоренца, относятся к разряду явлений и не всегда совпадают с действительными параметрами и характеристиками, измеренными в системе отсчета, связанной с исследуемым объектом. Однако при преобразовании Лоренца некоторые величины остаются неизменными (инвариантными). Среди них:

1. Сохраняется действительное равноправие всех инерциальных систем отсчета.

2. Физическое время остается общим и единым для всех ИСО. Это единое мировое время.

3. Общим для всех ИСО остается трехмерное пространство.

4. Скорость света и сечение светового луча остаются неизменными (инвариантными) для всех ИСО.

Наблюдаемые "замедление" времени и "сжатие" масштаба - суть объективные явления, т.е. искаженные отображения истинного темпа времени (единого для всех ИСО) и масштаба координатной оси пространства (общего для всех ИСО).

Уже сам принцип равноправия инерциальных систем предполагает, например, единство времени во всех ИСО. В противном случае различие в темпах изменения времени могло бы служить критерием для дифференциации различных ИСО.

6. Наблюдаемая и истинная скорость объекта

Хотя этот вопрос уже обсуждался нами в [1], [2], [3], мы вновь рассмотрим вопрос о наблюдаемой (явление) и истинной (характеристика сущности) скоростях частиц и их различии, поскольку этот вопрос имеет важнейшее значение для физики.

Пусть мимо наблюдателя по прямой линии движется материальная точка со скоростью v. В собственной системе отсчета K' (ее координата x' постоянна) она дает световые вспышки через равные интервалы времени Δt_o . Эти вспышки регистрируются неподвижным наблюдателем в системе K. Мы можем мысленно представить прямолинейную траекторию, которая как бы разбита на равные отрезки длиной Δx светящимися точками. За время Δt_o система К успеет переместиться относительно K' на это расстояние Δx.

Используя преобразования Лоренца, найдем расстояние Δx между вспышками.

,

где ΔТ это наблюдаемое в системе К время между двумя вспышками, определенное с помощью преобразования Лоренца

.

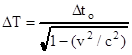Введем угол θ, образованный двумя векторами: вектором скорости v, направленным вдоль оси x, и вектором направления световых лучей от движущегося объекта к наблюдателю. Благодаря эффекту Доплера наблюдаемый интервал между световыми вспышками будет также зависеть от угла наблюдения θ. Учитывая искажение интервалов времени эффектом Доплера, найдем наблюдаемый интервал времени между вспышками, которые видны под углом θ в системе К. Он равен:

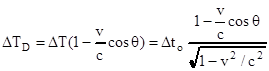
где ΔТ_D - наблюдаемый интервал времени между вспышками, искаженный эффектом Доплера; ΔТ- тот же наблюдаемый интервал времени, когда θ=90^о .

Теперь, выражая в (6.1) интервал Δt_o через ΔТ_D , получим:

.

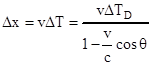Отсюда нетрудно найти наблюдаемую (кажущуюся) скорость, которая зависит от угла наблюдения θ:

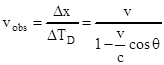
Полученный результат имеет интересные следствия.

Во-первых, мы будем видеть неравномерное движение источника световых импульсов, скорость которого постоянно уменьшается. Наблюдаемое "ускорение" равно

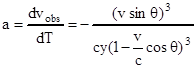
где у - координата движущейся точки.

В частности, при θ=90^о ускорение равно .

Это ускорение существует "на самом деле" или же нам это "кажется" (объективная "кажимость")? Означает ли это, что на движущуюся частицу действуют какие-то силы? "Реальны" ли эти силы или же они тоже "кажущиеся"? Как быть с принципом причинности?