Доклад: Моделювання поведінки виробників та споживачів

1. МОДЕЛІ ПОВЕДІНКИ СПОЖИВАЧІВ

В теорії споживання вважається, що споживач керується принципом рацiональностi: вiн завжди прагне максимізувати свою корисність, i єдине, що його стримує, — це обмежений дохід:

max u(x) (1.1)

px = M

де х=(х₁ ,...,х_n )′ – вектор-стовпчик обсягів споживчих товарів, що придбав споживач за заданих цін; n – число різноманітних товарів; u(х) – функція корисності споживача; р = (p₁ ,…,p_n ) – вектор-рядок цін товарів; М – обсяг доходу споживача.

Це задача на умовний екстремум, i її розв’язок зводиться до знаходження безумовного екстремуму функції Лагранжа:

L(x,λ)=u(x)-λ(px-M) .

Необхідними умовами локального екстремуму є:

(1.2)

(1.3)

Точка екстремуму справді визначає точку максимуму, оскільки матриця Гессе U(х)=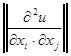 є вiд’ємно визначеною. З виразу (1.3) бачимо, що споживач за фіксованого доходу так обирає набір , що в цій точці відношення граничної корисності дорівнює відношенню цін:

Якщо розв’язати (1.2), (1.3) відносно , отримаємо функцію попиту споживача:

2. РІВНЯННЯ СЛУЦЬКОГО

Розглянемо, як зміниться попит споживача, що визначається моделлю (1.1), якщо зміниться ціна одного з товарів. Нехай ціна n -го товару зросла на . Це приводить до такої зміни попиту на товари

(2.1)

де р – вектор-рядок цін; U – матриця Гессе; – вектор-стовпчик попиту на товари; – множник Лагранжа; – індекс n за дужками біля матриці означає, що взято й n -й стовпчик.

Проаналізуємо зміст складових, що входять у рівняння (2.1).

Зміна попиту за збільшення ціни з компенсацією доходу. Нехай дохід споживача збільшився на таку величину , яка компенсує споживачеві збільшення ціни на n -й товар (благо) на .

Збільшення ціни з компенсацією доходу приводить до такої зміни попиту:

(2.2)

Тобто друга складова у правій частині рівняння (2.1) — це зміна попиту, якщо зростання ціни n -го товару на компенсується збільшенням доходу на .

Зміна попиту за зміни доходу. Якщо дохід змінюється на , то відповідно змінюється попит:

(2.3)

Об’єднуючи вирази (2.1), (2.2), (2.3), отримаємо рівняння Слуцького, яке є серцевиною теорії корисності:

(2.4)

Оскільки вивчається зміна попиту за зростання ціни на n -й товар, що не компенсується підвищенням доходу, то друга складова в (2.4) (з від’ємним знаком) знімає штучний приріст по спричинений компенсуючим зростанням доходу.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--