Доклад: Резонансные частицы
Ниже мы покажем, что протон - это квантовый гармонический осциллятор с замкнутыми петлями.
В работе [1] показано, что ядерное поле протона входит в структуру частиц. Частицы слоистые, и слои вращаются с частотой де Бройля. Квантовый радиус протона ![]() см. Это есть радиус квантовых сил.
см. Это есть радиус квантовых сил.
В работе [2] показано, что ядерное поле обладает свойством упругости. Сила упругости, как было определено, есть
![]() (1)
(1)
где ![]() ,
, ![]() - масса протона, с - скорость электромагнитных волн (предельная скорость).
- масса протона, с - скорость электромагнитных волн (предельная скорость).
С другой стороны, ![]() , (2)
, (2)
где ![]() .
.
Из (1) и (2) получим: ![]() . При
. При ![]() имеем:
имеем:
![]() . (3)
. (3)
Потенциальная энергия ядерного поля протона, как известно из [1], есть 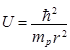 . Отсюда при
. Отсюда при ![]()
![]() получим
получим ![]() , где
, где ![]() - радиус ядра протона.
- радиус ядра протона.
Таким образом, ![]() - потенциальная энергия.
- потенциальная энергия.
Показано, что мезоны ![]() и т.д. - кванты ядерного поля. Верхние слои - пи-облака, ниже - ка-облака и т.д. При
и т.д. - кванты ядерного поля. Верхние слои - пи-облака, ниже - ка-облака и т.д. При ![]()
![]() = const, здесь
= const, здесь ![]() - Ньютонова связь.
- Ньютонова связь. ![]() растет к центру протона.
растет к центру протона.
Пусть ![]() - энергия поля, заключенная между
- энергия поля, заключенная между ![]() , тогда
, тогда ![]() =
= ![]() или
или ![]() , где
, где ![]() - период обращения слоев
- период обращения слоев ![]() .
.
Если ![]() - частота падающих частиц
- частота падающих частиц ![]() , частицы поглощаются слоем
, частицы поглощаются слоем ![]() и т.д. Протон имеет возбужденное состояние. Поэтому энергия осциллятора есть
и т.д. Протон имеет возбужденное состояние. Поэтому энергия осциллятора есть
![]() N = 0, 1, 2… (N - энергетические уровни).
N = 0, 1, 2… (N - энергетические уровни).
Здесь ![]() - кинетическая энергия вращательного движения,
- кинетическая энергия вращательного движения, ![]() - потенциальная энергия.
- потенциальная энергия.
Величина (N +![]() ) связана со спином резонансных частиц, т.е.
) связана со спином резонансных частиц, т.е. ![]() При N = 1
При N = 1 ![]() , при N = 2
, при N = 2 ![]() и т.д.
и т.д.
Таким образом, резонансные частицы - возбужденное состояние протона. Барионы - слияние ![]() с другими частицами, например, нейтрон
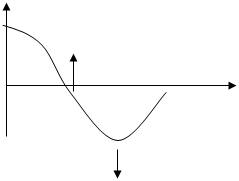
с другими частицами, например, нейтрон ![]() , и поэтому структура нейтрона такова [1]:
, и поэтому структура нейтрона такова [1]:
 е
е
![]()
+I
0 r
L-IIД где S = ![]() ,
,
![]()
![]() - магнитный момент нейтрона
- магнитный момент нейтрона
Отсюда можно сделать заключение, что в центре бариона находится протон, и в центре антибариона находится антипротон.
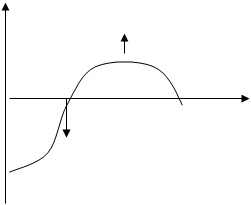
Антинейтрон имеет структуру:
![]()
L II Д
--> ЧИТАТЬ ПОЛНОСТЬЮ <--