Доклад: Закон тождества

ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

им. В. Н. КАРАЗИНА

Тема: Логика

Выполнил: Пригара С. Г.

Харьков 2007

ЗАКОН ТОЖДЕСТВА

ОБЪЕКТ И ИНФОРМАЦИЯ

Определим объект, как то, на что направлено некоторое действие – внимание, познание, применение, преобразование и др. В русском языке понятию объект ближе всего соответствуют термины предмет, сущность и вещь .

Согласно Н. Винеру нформация сама по себе не существует в материальном мире, она всегда связана с каким-либо объектом (носителем, источником, получателем, хранителем) и представляет собой продукт жизнедеятельности, в частности – функционирования человеческого сознания (восприятия, воспроизведения, мышления, памяти) и в то же время его атрибут, а по своей природе – занимает промежуточное положение между сознанием и средой. Информация может исчезнуть физически, если прекратят свое существование все объекты – ее носители.

Со всяким конкретным свяжем некоторый другой, абстрактный объект, содержащий информацию об исходном и включающий его уникальное имя и свойства (признаки, характеристики); будем предполагать, что каждому свойству соответствует некоторый метод, реализующее это свойство. Для выбранного действия изучения, объектом служит и сам человек, одно из его свойств – это мыш­ле­ние, отличающее его от неживой природы, методами которого служат законы логики.

Из сказанного следует, что для того чтобы исходный объект стал абстрактным необходимо, чтобы на него кто-нибудь обратил внимание и составил таблицу следующего вида.

Таблица 1

наименование объекта

свойство1

...

свойствоn

В таблице 2 приведен пример построения абстрактного объекта для предложения: «Харьков и Лубны лежат на одной параллели».

Таблица 2

параллель

Харьков

Лубны

Как видно из таблицы, «параллель» служит наименованием объекта , а «Харьков» и «Лубны» – его свойствами.

В таблице 3 приведен пример построения объекта-иден­тификатора для предложения: «В г. Харькове есть улицы – Пушкинская и Сумская».

Таблица 3

г. Харьков

ул. Пушкинская

ул. Сумская

ЭКВИВАЛЕНТНОСТЬ

Рассмотрим понятие эквивалентности (~) на множестве объектов X , как бинарное отношение, основанное на общности свойств, для которого выполнены следующие условия:

1. (рефлексивность ) "a Î X®a ~ a ,
2. (симметричность ) "а , b ÎX Ùa ~ b ®b ~ a ,
3. (транзитивность ) "а , b ÎX Ùa ~ b Ùb ~ c ®a ~ c .

В частности, отношение эквивалентности – это равенство (=) или (»), подобие геометрических фигур и др. Неравен­ст­во (¹) и сравнения (><) не явлются отношениями эквивалентности.

Обозначим через α= {α} заданное множество свойств и значений переменных исходных объектов. Определим предикат А_α :

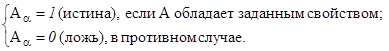
Для абстрактного объекта А , соответствующего исходному, "α Îα ® А_α = 1. Таким образом любой объект включает множество свойств α = {α} и определенную на нем логическую функцию А_α .

Рассмотрим два оъекта А, В и некоторое свойство α, определим отношения эквивалентности и неравен­ства двух объектов:

$α ÎαÙ А_α = В_α « А ~ В (эквивалентность );

$α Îα ÙА_α ¹ В_α « А ¹ В (неравенство ).

Понятие эквивалентности от А_a = В_a обобщается для (класс э . {А} или {А }), например по признаку геметрического подобия эквивалентными оказываются футбольный мяч, планета земля и светило солнце; оно имеет синоним – общность. Пусть {C} – клас эквивалентности, С – его объект-идентификатор. Определим отношение тождества , как: с º С« с Î {С}. В соответствии таким определением вышеназванные предметы тождественны с геометрической фигурой, именуемой – шар.

Эквивалентность связана с различными языковыми понятиями и отношениями в материальном мире и на самом деле означает абстрагирование тех или иных свойств. Ее примерами служат различные собирательные (молодость,стереотип, дружба) и методические термины (класс, стандарт) или языковые синонимы и антонимы – все они на самом деле означают общее наименование групп предметных понятий, объединяемых по тем или иным признакам. К эквивалентностям относятся и известные конструкции, вроде – съесть ложку или выпить чашку (правильно – съесть ложку кашу, выпить чашку чая), например:

– Еще тарелочку; послушай:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--