Контрольная работа: Анализ и моделирование цифровых и аналоговых схем

Для выполнения анализа схемы необходимо разработать ее синхронную модель в двоичной логике. Математическая модель заданной схемы имеет вид:

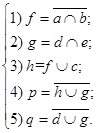
Для реализации анализа по методу простой итерации необходимо задать начальное приближение для вектора выходных переменных Y₀ =(f,g,h,p,q). Для расчета начальных приближений вектора выходных переменных воспользуемся начальным значением вектора входных переменных X=(a,b,c,d,e)=(00100), предварительно расположив уравнения в порядке прохождения сигналов по схеме:

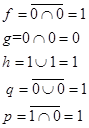
Y₀ =(f,g,h,p,q)=( 1,0,1,1,1).

Метод простой итерации состоит в выполнении итераций по формуле:

Y_i = y (Y_i-1 , X),

где Y_i - значение вектора Y на i -й итерации, т.е. при вычислении Y₁ в правые части уравнений модели поставляются значения выходных переменных из начального приближения Y₀ , при вычислении Y₂ – значения из результата первой итерации Y₁ и так далее. Если Y_i =Y_i-1 , то решение найдено; если

Y_i ¹ Y_i-1 , то выполняется новая итерация; если итерационный процесс не сходится, то это свидетельствует об ошибках проектирования схемы устройства, вызывающих неустойчивость его состояния.

Результат анализа заданной схемы по методу простой итерации приведен в таблице 3.

Таблица 3

№ итерации	Начальное приближение Y0
	g	p	f	h	q
	0	1	1	1	1
1 2	0 0	1 1	0 0	1 1	1 1

Из таблицы 3 видно, что потребовалось два раза обращаться к каждому из пети уравнений модели, прежде чем результат второй итерации, совпадающий с результатом первой итерации, показал, что решение найдено.

Таким образом, искомое значение вектора выходных переменных при изменении X=(a,b,c,d,е) с 00100 на 11101 для заданной схемы равно:

Y=(e,g,p,f,h,q)=(0,1,0,1,1).

При использовании событийного метода вычисления на каждой итерации выполняются только по уравнениям активизированных элементов, т.е. элементов, у которых хотя бы на одном входе произошло событие (изменилась входная переменная). В алгоритме событийного метода на каждом шаге вычислительного процесса имеется своя группа активизированных элементов.

В заданном варианте изменения вектора входных переменных изменяются только значения переменных а, b и е , следовательно, на первой итерации при реализации событийного алгоритма анализа должны быть пересчитаны только выходные переменные f и h , в правые части уравнений которых входят аргументами b и d . Если по результатам вычисления значения f и h совпадут с начальным приближением, то решение будет найдено, если хотя бы одна из этих переменных изменится, то на второй итерации должны быть пересчитаны те выходные переменных, в правые части уравнений которых входят изменившиеся в результате первой итерации переменные. Процесс продолжается до тех пор, пока в результате очередной итерации значения рассчитываемых переменных не совпадут с их предыдущими значениями, т.е. до выполнения условия Y_i =Y_i-1 .

Результат анализа заданной схемы по методу простой итерации приведен в таблице 4.

Таблица 4

№ итерации	Начальное приближение Y0						Изменяющиеся переменные	Активизированные уравнения
	e	g	p	f	h	q
	0	0	1	1	1	0
0 1 2 3 4 5 6	0	0 1	1 1 0	1 0	1 1 0	0 1 1	b, d f g h q p -	4 и 5 2 5 6 3 6 -
Результат	0	1	0	0	0	1

Как видно из таблицы 4, на 6-ой итерации результат расчета переменной q совпал с ее предыдущим значением, следовательно решение найдено.

Таким образом, искомое значение вектора выходных переменных при изменении X=(a,b,c,d) с 0110 на 0011 при расчете по событийному методу для заданной схемы совпадает с результатом анализа по методу простой итерации и равно:

Y=(e,g,p,f,h,q)=(0,1,0,0,0,1).

Однако, при вычислении по методу простой итерации, потребовалось на каждой итерации вычислять все выходные переменные, т.е. объем вычислений составил 6×6=36 операций. Тот же результат при использовании событийного метода потребовал значительно меньшего объема вычислений, а именно выполнения 8 операций. Таким образом, трудоемкость событийного метода значительно меньше.

Задача №3. Анализ цифровых схем по методам Зейделя

Задание: выполнить анализ заданной схемы по методам Зейделя для заданного изменения вектора входных переменных.

Исходные данные:

Схема:

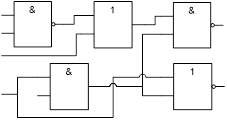
Заданный вариант изменения вектора входных переменных:

X=(a,b,c,d,e) меняет свое значение с 00100 на 11101