Чергове k-е наближення:

В якості малої величини беремо задану точність обчислень , тоді розрахункова формула має вигляд:

При уточненні коренів рівняння методом січних користуємось наступними формулами:

Для першого наближення:

Для подальших наближень:

Завдання № 3,4

Наближення функцій поліномами вищого порядку

Функція y=f(x) задана таблицею значень у точках . Використовуючи метод найменших квадратів (МНК), знайти многочлен найменшого середньоквадратичного наближення оптимальної степені m=m*. За оптимальне значення m* прийняти ту степінь многочлена, починаючи з якої величина стабілізується або починає зростати.

Вихідні дані:

Варіант 2
x	0	0,375	0,563	0,75	1,125	1,313	1,5	1,690	1,875	2,063	2,25	2,438	2,625	2,813	3
y	4.568	3,365	2,810	2,624	0,674	0,557	0,384	-0,556	-1,44	-1,696	-1,91	-2,819	-3,625	-3,941	-4,367

Хід виконання:

1. Задаємо вектори x та y вихідних даних.

2. Використовуючи метод найменших квадратів, знаходимо многочлени Pm, m = 0,1,2... Розраховуємо відповідні їм значення .

3. Будуємо гістограму залежності від m, на основі якої вибратємо оптимальну степінь m* многочлена найкращого середньоквадратичного наближення.

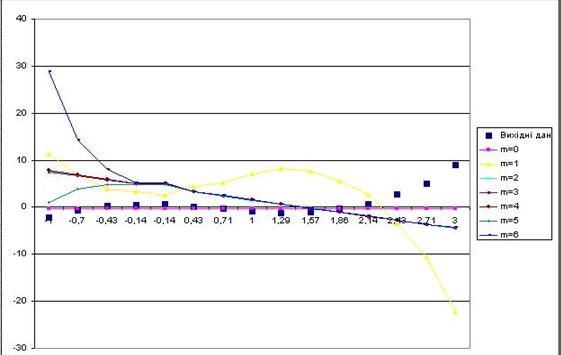
4. На одному графіку будуємо многочлени P_m , m = 0,1,2,..., m*, і точковий графік вихідної функції.

Реалізація у MS Excel:

Визначаємо матрицю Х як суму відповідних х_і у відповідних степенях та у_і *х_і ^j

За допомогою отриманих даних, будуємо, для полінома кожної степені, відповідну матрицю Х:

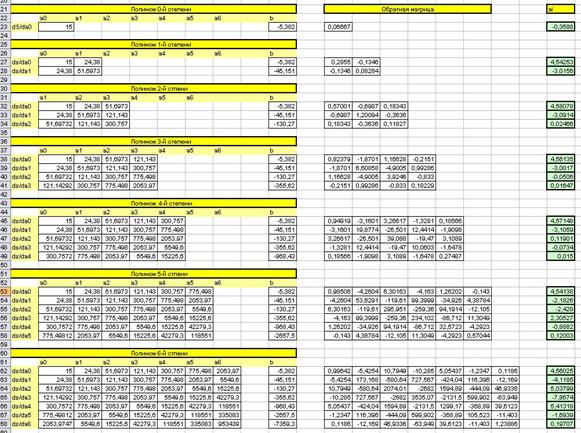
Визначаємо обернені матриці Х^-1 до відповідних матриць Х, використовуючи вбудовану функцію Excel МОБР(....).

Визначаємо коефіцієнти відповідних поліномів, для чого визначаємо добуток матриць Х^-1 та B, використовуючи вбудовану функцію МУМНОЖ(....).

Використовуючи визначені коефіцієнти поліномів а_і , визначаємо значення даних поліномів у кожній точці х_і .

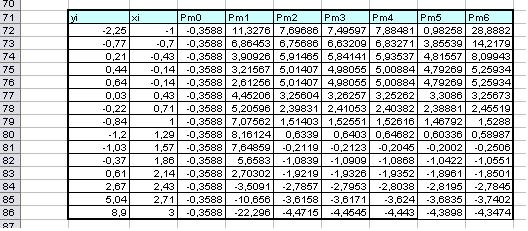
Будуємо графік отриманих поліномів та вихідних даних: вихідні дані – точковий графік, розрахункові дані – лініями різного типу.

Визначаємо величину для кожного полінома та будуємо гістограму: