Контрольная работа: Числові методи

Виконав

студент 2-го курсу

кафедри ЕОМ

Перевірив

м. Чернівці

Завдання 1

Задана СЛАР

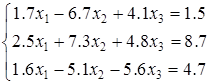
а) розв’язати цю систему методом Гауса за схемою з частковим вибором головного елементу;

б)розв’язати цю систему за формулою

.

– вектор невідомих, – вектор вільних членів, – обернена матриця до матриці з коєфіцієнтів при невідомих.

Обернену матрицю знай ти методом Гауса - Жордана за схемою з частковим вибором головного елемента.

Рішення.

а) Прямий хід методу Гауса.

()

Запишемо матрицю .

1-й крок.

Серед елементів першого стовпчика шукаємо максимальний:

Перше і друге рівняння міняємо місцями.

Розділимо рівняння (1) на 2.5

(1)

Від рівняння (2) віднімемо 1.7Р1 .

(2)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--