Контрольная работа: Деякі формати мультимедіа. Використання шейдерів та фракталів
Формат MPEG-4 почали розробляти ще в першій половині 90-х років минулого століття. Як основу формату файлу були прийняті розроблені Apple Computer алгоритми формату QuickTime. У 1998 р. була випущена перша версія MPEG-4, у грудні 1999 року був представлений реліз цього формату, що одержав офіційний статус стандарту ISO/IEC (International Standards Organization/International Electrotechnical Commission). MPEG-4 був задуманий як спосіб передачі потокових медіа-даних, у першу чергу відео, каналами з низькою пропускною здатністю. Слід зазначити, що MPEG-4 — окремий стандарт ISO/IEC-14496, що застосовується в тих областях, де використання форматів MPEG-1 і MPEG-2 не є ефективним. На відміну від MPEG-1 і MPEG-2, що здійснювали тільки ущільнення й декомпресію аудіо- та відеосигналів, MPEG-4 забезпечує інтерактивну передачу потокових медіа-даних — створення й доставку мультимедійної цифрової інформації Інтернетом на комп'ютери, а також на мобільні пристрої.
2. Шейдери та фрактали
Розвиток методів і технологій текстурування та намагання використовувати гнучкі процедурні методи зафарбовування призвели до появи поняття шейдер. Шейдер (від англ. shade — затемнювати, тут не плутати shade із shadow — тінь, шейдер затемнює, а не затінює — для генерації тіней від об'єктів у графіці використовуються доки що не шейдери, а інші засоби) — це невеличка програма, яка містить набір інструкцій для розрахунку кольорів пікселів об'єктів у ході циклу візуалізації. Фактично, шейдери трохи в іншому вигляді використовувалися вже давно в графічних пакетах для створення спецефектів у кіно (наприклад, у пакеті Maya). При створенні спецефектів для запису кадрів кінофільму не дуже потрібен режим реального часу, кожний кадр може генеруватися хвилину та довше, головне тут — це якість зображення.
У 2001-2002 pp. для масового вжитку, в першу чергу для комп'ютерних ігор, почали виготовлятися відеоадаптери (nVidia GeForce3,. ATI Radeon 8500), які апаратно підтримують базові операції шейдерів. Розробники графічних програм зацікавилися гнучкими можливостями шейдерів, оскільки відчувалася обмеженість фіксованого набору процедур графічного конвейєра. Можливість програмування графічних процесорів дає новий поштовх розвитку засобів комп'ютерної графіки. На рис. 3.34 наведено приклад зображення хвиль, створеного за допомогою шейдерів.

Сучасні графічні процесори здатні виконувати для кожного піксела десятки й сотні шейдерних команд у реальному часі.
Зараз існує два типи шейдерів — вершинні {vertex shaders) та піксельні (pixel shaders). Вершинні шейдери призначені для обчислення координат вершин полігонів та виконання розрахунків освітлення, наприклад, методом Гуро. Їх можна вважати доповненням можливостей апаратних засобів T&L (transform and lighting). Вершинний шейдер може обробляти всі дані, що стосуються одної вершини — координати вершини, координати нормалі, текстурні координати, колір, освітлення тощо.
Піксельні шейдери з'явилися спочатку як спосіб опису накладання пікселів багатошарових текстур. Тепер вони містять різноманітні операції визначення кольорів окремих пікселів. Шейдери оперують такими типами даних — цілі числа, числа з плаваючою точкою, трійки RGB, вектори, матриці.
Наведемо формат однієї команди шейдера для DirectX 8
![]()
де: op— ім'я команди,
dest — регістр, в який записується результат,
src0, srcl, src2 — регістри вхідних даних.
Як бачимо, мова команд шейдерів фактично є асемблером. Для розробки шейдер-них програм можна використовувати API DirectX (8.0 та наступних версій), OpenGL 2.0 (шейдерні операції частково підтримуються в розширеннях OpenGL версій 1.2 та 1.3). Також розроблені спеціальні мови програмування для шейдерів — це Cg (nVidia) та Monkey (ATI) [98].
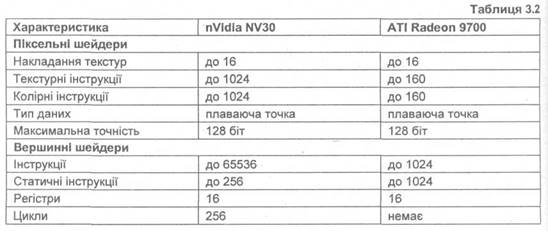
Загальні відомості про шейдерні можливості сучасних відеоадаптерів надані у таблиці 3.2
Фрактал можна визначити як об'єкт досить складної форми, який отримано в результаті виконання простого ітераційного циклу. Ітераційність, рекурсивність обумовлюють такі властивості фракталів, як самоподібність — окремі частини схожі за формою на весь фрактал у цілому. Латинське fractus означає "складений із фрагментів". У 1975 році французький математик Бенуа Мандельброт видав книгу "The fractal Geometry of Nature" [38]. Відтоді слово "фрактал" стало модним.
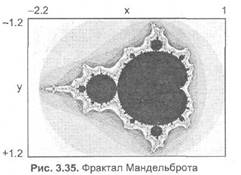
Фракталом Мандельброта названо фігуру, яка породжується дуже простим циклом. Для створення цього фрактала необхідно для кожної точки зображення виконати цикл ітерацій згідно з формулою:
![]()
де k = 0, 1,..., п. Величини zk — це комплексні числа, zk = xk + iyk, причому стартові значення х0 та у0 — це координати точки зображення. Для кожної точки зображення ітерації виконуються обмежену кількість разів (n) або доти, доки модуль числа zk не перевищує 2. Модуль комплексного числа дорівнює кореню квадратному з х2 + у2. Для обчислення квадрата величини zk можна скористатися формулою z2 = (х + іу) (х + іу) = (х2 - у2) + і(2у), оскільки і2 = -1. Цикл ітерацій для фракталу Мандельброта можна виконувати в діапазоні х = (від -2.2, до 1), у = (від -1.2 до 1.2). Для того щоб отримати зображення в растрі, необхідно перераховувати координати цього діапазону в піксельні (рис. 3.35).
Фрактал Джулія зовсім не схожий на фрактал Мандельброта, однак він визначається ітераційним циклом, майже повністю тотожнім циклу генерації Мандельброта. Формула ітерацій для фрактала Джулія така:
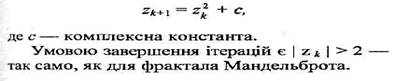
На рис. 3.36 зображено фрактал Джулія для с = 0.36 + і 0.36, п = 256.

Як бачимо, фрактал самоподібний — при будь-якому збільшенні окремі частини нагадують форми цілого. Самоподiбнiсть вважається важливою властивістю фракталів. Це відрізняє їх від інших типів об'єктів складної форми.
Розглянемо наступний приклад фрактала — фрактал Ньютон. Для нього ітераційна формула має такий вигляд:
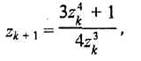
де z — також комплексні числа, причому z0 = х + іу відповідає координатам точки зображення.