Контрольная работа: Деякі формати мультимедіа. Використання шейдерів та фракталів

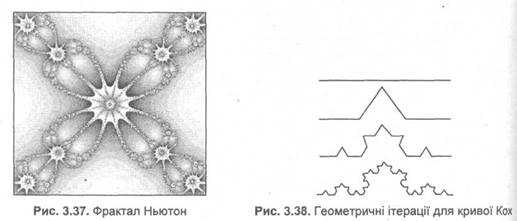
Розглянемо ще один різновид фракталів. Такі фрактали названо геометричними, оскільки їхня форма може бути описана як послідовність простих геометричних операцій. Наприклад, крива Кох стає фракталом у результаті безкінечної кількості ітерацій, в ході яких виконується поділ кожного відрізка прямої на три частини. На рис. 3.38 показані три ітерації — поступово лінія стає схожою на сніжинку.

Наступну групу складають фрактали, що генеруються відповідно до методу "систем ітеративних функцій" — IFS (Iterated Functions Systems). Цей метод може бути описаний, як послідовний ітеративний розрахунок координат нових точок у просторі:

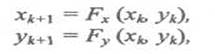
де Fx та Fy — функції перетворення координат, наприклад, афінного перетворення. Ці функції й обумовлюють форму фрактала. У випадку афінного перетворення необхідно знайти відповідні числові значення коефіцієнтів.

Давайте спробуємо розробити фрактал, який виглядав би, як рослина. Уявимо стовбур, на якому багато гілочок. На кожній гілочці багата менших гілочок і так далі. Найменші гілки можна вважати листям або колючками. Усі елементи будемо рисувати відрізками прямої. Кожен відрізок визначатиметься двома кінцевими точками.

Для початку ітерацій необхідно задати стартові координати кінців відрізку. Це будуть точки 1, 2. На кожному кроці ітерацій будемо розраховувати координати інших точок.

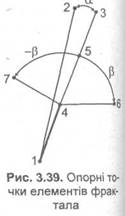
Спочатку знаходимо точку 3. Це повернута на кут а точка 2, центр повороту — в точці 1 (рис. 3.39):

Якщо = 0, то стовбур та всі гілки прямі. Потім знаходимо точку 4. Від неї будуть розповсюджуватися гілки. Нехай співвідношення довжин відрізків 1-4 та 1-3 дорівнює к, причому 0 < к < 1. Тоді для обчислення координат точки 4 можна скористатися такими формулами:

Тепер задамо довжину та кут нахилу гілок, що виходять із точки 4. Спочатку знайдемо координати точки 5. Уведемо ще один параметр — к1, який визначатиме співвідношення довжин відрізків 4-5 та 4-3, причому також 0 < к1 < 1. Координати точки 5 дорівнюють

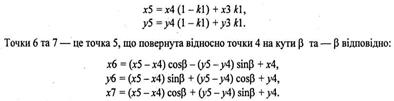
Окрім розрахунку опорних точок, на кожному кроці будемо рисувати один відрізок 1-4. В залежності від номера ітерацій можна змінювати колір відрізка. Також можна встановлювати його товщину, наприклад, пропорційно довжині.

Таким чином, фрактал ми визначили як послідовність афінних перетворень координат точок. Величини , , к, к1 — це параметри, які описують вигляд фрактала в цілому. Вони є константами на протязі усього ітеративного процесу. Це дає можливість в ітераціях використовувати тільки операції додавання, віднімання та множення, якщо обчислити значення sin(), cos(), (1 - к) та (1 - kl) тільки один раз перед початком ітерацій у вигляді коефіцієнтів-констант.

Дамо запис алгоритму у вигляді рекурсивної процедури крок ():

Для того щоб нарисувати фрактал, необхідно викликати процедуру КРОК, встановивши відповідні значення її аргументів: крок(xl, yl, х2, у2, 0). Зверніть увагу на один з аргументів цієї процедури — пит, який спочатку має значення 0. У тілі процедури є три рекурсивних виклики з різними значеннями цього аргументу:

• крок(х4, у4, х3, у3, num)—продовжуємо стовбур;

• крок(х4, у4, х6, у6, num+l)—права гілка;

• крок(х4, у4, х7, у7, num+l) —ліва гілка.

Значення пит показує ступінь деталізації обрахування дерева. Один цикл ітерацій містить багато кроків, що відповідає одному значенню величини num. Числове значення пит можна використовувати для припинення ітеративного процесу, а також для визначення поточного кольору елементів "рослини".

Завершення циклів ітерацій у нашому алгоритмі відбувається тоді, коли довжина гілки стає менше від деякої величини lmin , наприклад, lmin = 1.

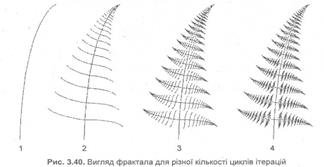
Цей фрактал при = 2°, = 86°, к = 0.14, к1 = 0.3 схожий на папороть (рис. 3.40).

Метод IFS використовується не тільки для створення зображень. Його використали Барнслі та Слоан для ефективного ущільнення графічних зображень при записі до файла. Основна ідея така: оскільки фрактали можуть репрезентувати дуже складні зображення за допомогою простих ітерацій, то опис цих ітерацій потребує значно меншого обсягу інформації, ніж відповідні растрові зображення. Дkя кодування зображень необхідно вирішувати обернену задачу — для зображення (або його фрагмента) підібрати відповідні коефіцієнти афінного перетворення. Цей метод використовується для запису кольорових фотографій у файли з ущільненням у десятки і сотні разів без помітного погіршення зображення. Формат таких графічних файлів було названо FIF (Fractal Image Format) і запатентовано фірмою Iterated Systems [40].

3. Засобами бібліотеки Opengl активізувати джерело світла на формі . Забезпечити операцію масштабування використовуючи клавіші “+” та “-“