Контрольная работа: Дискретная теория поля
2. 
, k=const
3. 
4. Если поверхность разделена на части S1 и S2 , то
5. Если 
, то 
6. 
7. Теорема о среднем.
Если функция F(x, y, z) непрерывна в любой точке поверхности S, то существует точка (a, b, g) такая, что
S – площадь поверхности.
Какова бы ни была функция f(x, у, z), определенная в точках поверхности (S) и ограниченная:
,
имеет место равенство
в предположении существования одного из этих интегралов (что влечет за собой и существование другого).
Таким образом, для сведения поверхностного интеграла первого типа к обыкновенному двойному нужно лишь заменить координаты х, у, z их выражениями через параметры, а элемент площади dS— его выражением в криволинейных координатах.
Рассмотрим несколько примеров вычисления поверхностных интегралов.
Пример 1. Вычислить интеграл
по верхней стороне полусферы
Решение.
Преобразуем уравнение поверхности к виду:
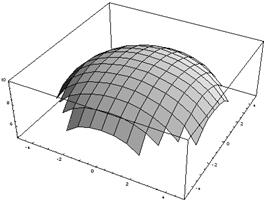
Заданная поверхность проецируется на плоскость XOY в круг, уравнение которого:
Для вычисления двойного интеграла перейдем к полярным координатам:
