Пример 2. Вычислить поверхностный интеграл 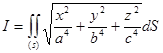распространенный на поверхность (S) эллипсоида:

.

Решение.

Если воспользоваться представлением эллипсоида:

, , ,

то элемент поверхности представиться в виде

.

С другой стороны, подынтегральная функция

.

По соображениям симметрии вычисление приводится к первому октану, так что

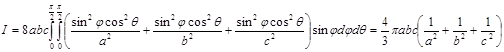
Поток векторного поля через поверхность.

По определению

.

Каждое слагаемое суммы

(*)

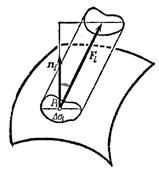
может быть истолковано механически следующим образом: это произведение равно объему цилиндра с основанием ,и высотой . Если вектор Fесть скорость жидкости, протекающей через поверхность а, то произведение (*) равно количеству жидкости, протекающей через площадку _; за единицу времени в направлении вектора (Рис. 3).

Выражение дает общее количество жидкости, протекающей в единицу времени через поверхность в положительном направлении, если под вектором Fподразумевать вектор скорости течения жидкости в данной точке. Поэтому поверхностный интеграл называется потоком векторного поля F через поверхность .

Из определения поверхностного интеграла следует, что если поверхность разбить на части , , ..., , то

Выразим единичный вектор я через его проекции на оси координат:

.

Подставляя в интеграл выражения векторов Fи n через их проекции, получим:

Произведение есть проекция площадки на плоскость Оху; аналогичное утверждение справедливо и для произведений:

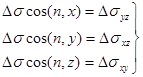
где , ,

проекции площадки на соответствующие координатные плоскости.