Контрольная работа: Дисперсія імпульсів в одномодових волокнах
Рівняння (1) показує, що Dl, по суті, пропорційно d2 b/dk0 . Щоб зробити оцінку величини s в східчастому одномодовому волокні, що для слабо спрямовуючих волокон (тобто для D<<1)
b@k0 n2 (1+2b). (3)
Рівняння (3) показує, що постійна розповсюдження b моди, по суті, має дві компоненти: перша пов'язана з чисто матеріальною спроможністю волокна (k0 n2 ) і друга пов'язана з хвильоводним (модовим) параметром b. Заради простоти, якщо ми розглянемо першу у відсутності другої, тоді, вважаючи тільки другий член (що відповідає хвильоводній дисперсії) в (3), одержимо
![]() . (4)
. (4)
Таким чином
 . (5)
. (5)

Рисунок 1 – Залежність дисперсії одномодового волокна від довжини хвилі
Дисперсія (в одномодовому волокні) в залежності від довжини хвилі приведена на рисунку 1. Крива матеріальної дисперсії відповідає легованому SiO2 -волокну (3,0 моля % GeO2 ), а крива хвильоводної дисперсії отримана розрахунковим шляхом - відніманням матеріальної дисперсії від загальної дисперсії.
Включаючи (4) в (5), одержуємо:
 , (6)
, (6)
де wg позначає "хвильоводний", щоб показати, що (6) представляє внесок в часову дисперсію в одномодовому волокні шляхом хвильоводної властивості волокна. Відповідно, Swg ´L називається хвильоводною дисперсією. Хоча, строго кажучи, щоб розрахувати Swg , треба вирішити для l=0 (відповідає моді LP01 ), щоб одержати b, і, таким чином, Vd2 (Vb)/dV2 при певних V в межах одномодової області. Можна також використати таке емпiричне рівняння для розрахунку Vd2 (Vb)/dV2 :
Vd2 (Vb)/dV2 »0,80+0,549(2,834-V)2 . (7)
Виходячи з подібної процедури зневаги другим членом в (6), можна показати, що внесок в дисперсію моди від впливу матеріалу дається шляхом:
 , (8)
, (8)
де Sm - коефіцієнт матеріальної дисперсії. Цікаво, що в оптичних волокнах телекомунікації, що звичайно засновані на чистому сплаві SiO2 у вигляді оболонки, Sm переходить через нуль при l0 @1,27 мкм (![]() ), який зміщається до більш довших хвиль (більш коротких l, в разі додання F або B) в легованому волокні SiO2 , як показано на рисунку 1 (крапкова крива, для якої
), який зміщається до більш довших хвиль (більш коротких l, в разі додання F або B) в легованому волокні SiO2 , як показано на рисунку 1 (крапкова крива, для якої ![]() @1,285 мкм). Хвильоводна дисперсія також зображена на тому ж рисунку як пунктирна крива, яка відповідає одномодовому волокну, що має діаметр 7,0 мкм і містить 3,0 моля % GeO2 легованого волокна SiO2 з плавленим SiO2 у вигляді оболонки. Загальна дисперсія (=Sm +Swg ) показана як товста крива на тому ж рисунку. Видно, що при
@1,285 мкм). Хвильоводна дисперсія також зображена на тому ж рисунку як пунктирна крива, яка відповідає одномодовому волокну, що має діаметр 7,0 мкм і містить 3,0 моля % GeO2 легованого волокна SiO2 з плавленим SiO2 у вигляді оболонки. Загальна дисперсія (=Sm +Swg ) показана як товста крива на тому ж рисунку. Видно, що при ![]() мкм, більшій, ніж 1,28 мкм, загальна внутримодова дисперсія проходить через 0. Ця довжина хвилі
мкм, більшій, ніж 1,28 мкм, загальна внутримодова дисперсія проходить через 0. Ця довжина хвилі ![]() , з повною дисперсією, яка дорівнює 0, відома в літературі як довжина хвилі нульової дисперсії. Змінюючи концентрацію домішок та хвильоводних параметрів, наприклад діаметру серцевини, можливо зробити падіння
, з повною дисперсією, яка дорівнює 0, відома в літературі як довжина хвилі нульової дисперсії. Змінюючи концентрацію домішок та хвильоводних параметрів, наприклад діаметру серцевини, можливо зробити падіння ![]() де-небудь в межах вікна довжин хвиль мінімальних втрат: 1,3 та 1,6 мкм для волокон з SiO2 , на довжинах хвиль, на яких працюють системи другого і першого поколінь. Таким чином, якщо волокно розроблено таким чином, що його
де-небудь в межах вікна довжин хвиль мінімальних втрат: 1,3 та 1,6 мкм для волокон з SiO2 , на довжинах хвиль, на яких працюють системи другого і першого поколінь. Таким чином, якщо волокно розроблено таким чином, що його ![]() співпадає з довжиною хвилі мінімальних втрат, можна досягнути надзвичайно великих інтервалів трансляції - понад 100 км, при високій пропускній спроможності в 4,2 Гбiт/с. Ми можемо визначити тут, що припущення про те, що хвильоводна і матеріальна дисперсії поділяються як самостійні ефекти, є гарним наближенням, якщо не вимагається дуже точне рішення при якій-небудь конкретній ситуації.
співпадає з довжиною хвилі мінімальних втрат, можна досягнути надзвичайно великих інтервалів трансляції - понад 100 км, при високій пропускній спроможності в 4,2 Гбiт/с. Ми можемо визначити тут, що припущення про те, що хвильоводна і матеріальна дисперсії поділяються як самостійні ефекти, є гарним наближенням, якщо не вимагається дуже точне рішення при якій-небудь конкретній ситуації.
Було б цінним визначити, що термін "нульова дисперсія" не є правильним в широкому сенсі, бо на цій довжині хвилі дисперсія перетворюється на 0 лише в першому порядку. Якщо ![]() спрямується до нуля, тоді член
спрямується до нуля, тоді член ![]() визначить дисперсію другого порядку, що залишилася. Цей другий порядок дисперсії може бути також в принципі подоланий фазовою компенсацією в приймачі за допомогою гетеродину в детекторі. Відповідно, максимальна теоретично можлива ширина смуги в одномодовому волокні при мінімумі дисперсії (на відповідній довжині хвилі) буде визначатися четвертим порядком похідної b по k0 і приблизно складати на довжині хвилі 1,3 мкм:
визначить дисперсію другого порядку, що залишилася. Цей другий порядок дисперсії може бути також в принципі подоланий фазовою компенсацією в приймачі за допомогою гетеродину в детекторі. Відповідно, максимальна теоретично можлива ширина смуги в одномодовому волокні при мінімумі дисперсії (на відповідній довжині хвилі) буде визначатися четвертим порядком похідної b по k0 і приблизно складати на довжині хвилі 1,3 мкм:
BW÷max *L0,25 =3TГц(км)0,25 . (9)
Якщо індекс профілю відхилявся від нього, наприклад, маючи осьовий провал індексу чи градієнтну форму профілю, передбачена повна дисперсія буде змінюватися як і l0 заг Гемблiнг та інш. вивчили дисперсію в одномодовому волокні з градієнтним профілем серцевини, вважаючи, що профіль показника заломлення одномодового волокна задається шляхом:
 , (10)
, (10)
де D¢@(n1 -n2 ) / n2 . Після алгебраїчних перетворень, внутрішньомодова дисперсія в таких волокнах буде визначатися як:
![]() , (11)
, (11)
де комплексний коефіцієнт матеріальної дисперсії
Scmd 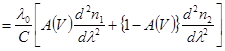 ; (12)
; (12)
(коефіцієнт хвильової дисперсії)
Swd 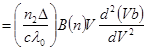 ; (13)
; (13)
(комплексний коефіцієнт дисперсії профілю)
Scpd ![]() ; (14)
; (14)
![]() , (15)
, (15)