Контрольная работа: Доказательство бесконечности некоторых видов простых чисел
последняя известная нам пара простых чисел-близнецов этого вида. Используя формулы (3) мы увидим, что все простые числа от ![]() до
до ![]() выбивают
выбивают
![]() (8)
(8)
часть чисел(6). А , используя формулу (4) мы получим, что на все остальные простые числа останется
![]() (9)
(9)
часть чисел (6).
Для того, чтобы выяснить есть ли еще другие пары простых чисел-близнецов в последовательности (6) больше за (7), достаточно исследовать формулу (9) на промежутке до ![]() .
.
Если
![]() (10)
(10)
где А-количество пар чисел (6) на промежутке от ![]() до
до ![]() ,тогда на этом промежутке есть еще хотя бы одна пара простых чисел-близнецов данного вида
,тогда на этом промежутке есть еще хотя бы одна пара простых чисел-близнецов данного вида
Так как
тогда последнее число вида (7) меньше ![]() , которое будет делиться простыми числами меньшими за
, которое будет делиться простыми числами меньшими за ![]() , будет число
, будет число
![]() .
.
С учетом этого формула (10) примет вид
![]() ,
,
где видно, что левая часть больше единицы, а это значит, что количество пар простых чисел-близнецов бесконечно.
Для примера рассмотрим простые числа-близнецы вида ![]() .
.
Пусть ![]() наибольшая пара таких чисел. Так как числа такого вида нечетные, значит,
наибольшая пара таких чисел. Так как числа такого вида нечетные, значит, ![]() не принимает участия. Выражение (10) для данного случая примет вид
не принимает участия. Выражение (10) для данного случая примет вид ![]() , где очевидно, что оно больше единицы, а это значит, что количество пар простых чисел-близнецов вида
, где очевидно, что оно больше единицы, а это значит, что количество пар простых чисел-близнецов вида ![]() бесконечно. Таким же способом можно рассматривать и более сложные многочлены первой степени. Очень легко доказывается и теорема Чебышева, Гольдбаха-Эйлера.
бесконечно. Таким же способом можно рассматривать и более сложные многочлены первой степени. Очень легко доказывается и теорема Чебышева, Гольдбаха-Эйлера.
Рассмотрим многочлен второй степени
![]() (11)
(11)
Делителями его будут простые числа вида
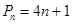 (12)
(12)
Подставляя в (11) значения ![]() от
от ![]() до
до ![]() получим ряд чисел
получим ряд чисел ![]() (13). Пускай
(13). Пускай ![]() наибольшее простое число вида
наибольшее простое число вида ![]() . Требуется доказать что есть еще простые числа вида
. Требуется доказать что есть еще простые числа вида ![]() больше за
больше за ![]() .
.
Каждое простое число (12) выбивает с последовательности (13)![]() часть чисел. С учетом формулы (3) мы получим, что все простые числа (12) от
часть чисел. С учетом формулы (3) мы получим, что все простые числа (12) от ![]() до
до ![]() выбивают
выбивают
![]() (14)
(14)
часть чисел с последовательности (13) На остальные простые числа вида ![]() останется с учетом формулы (4)
останется с учетом формулы (4)
![]() (15)
(15)
часть чисел последовательности (13).
Так как ![]() ,тогда последнее число вида
,тогда последнее число вида ![]() меньше
меньше ![]() , которое будет делиться простыми числами вида
, которое будет делиться простыми числами вида ![]() меньшим за
меньшим за ![]() , будет число
, будет число ![]() . .
. .
Для того ,чтобы показать, что есть еще простые числа
![]() (16)
(16)
достаточно доказать, что
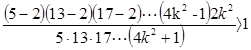 (17)
(17)
Для чего неравенство (17) запишем по-другому
![]() (18)
(18)