Контрольная работа: Дослідження однокрокових методів розвязання звичайних диференційних рівнянь

Даний метод є більш точним за прямий метод Ейлера так як його глобальна похибка складає 626846.

Метод Рунге-Кутта

Крок 0.1	Крок 0.05	Похибка
1.000000	1.000000	0.000000
1.229469	1.229644	0.000026
1.489718	1.489644	0.000103
1.783814	1.783663	0.000259
2.115130	2.114874	0.000524
2.487374	2.486981	0.000930
2.904625	2.904060	0.001513
3.371367	3.370593	0.002312
3.892533	3.891508	0.003370
4.473544	4.472224	0.004732

Даний метод є найточнішим серед прямого і зворотного методу Ейлера, його глобальна похибка дорівнює 0.004732.

Звідси можна зробити висновок; найбільш простим однокроковим методом, потребуючим мінімальних затрат розрахункових ресурсів, і який є дуже точним по відношенню до метода Ейлера є метод Рунге-Кутта. Метод Ейлера, крім значної похибки усічки, часто буває нестійким (малі локальні помилки приводять до значного збільшення глобальної).

4.1. Розв’язок диференціального рівняння в Mathcad

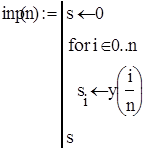
Звіримо результати обчислень. Візьмемо найточніший метод Рунге-Кутта та результат отриманий в Mathcad відповідно: 4.472 та 4.603 похибка 0.131

Тобто можна зробити висновок що результати обчислень програми і обчислення Mathcad майже співпадають.

5. Інструкція користувачу

Для завантаження необхідно переписати з дискети файл kursova.exe і запустити його, для роботи програми потрібен графічний драйвер egavga.bgi

Після завантаження слід натиснути клавішу Enter потрібну кількість разів щоб обрати потрібний метод

Після натиснення клавіші Esc відбудеться вихід з програми.

Висновки

В результаті виконання даної курсової роботи ми наглядно оцінили кожний з методів розв'язку диференційного рівняння і прийшли до висновку, що найточнішим методом з найменшою глобальною похибкою є метод Рунге-Кутта , а прямий метод Ейлера і зворотній метод Ейлера, є не досить точними. Але всі ці методи є простими однокроковими методами, що потребують мінімальні затрати розрахункових ресурсів. Тому можна сказати, що методи Ейлера краще використовувати для попередніх(приблизних) розрахунків, а щоб отримати точний результат можна застосувати більш точний метод Рунге-Кутта.

Література

1. В.Т.Маликов, Р.Н.Кветный . Вычислительные методы и применение ЭВМ . Учебное пособие -- К.: Высш. шк. Главное издательство,1989.-213 с .

2. В.Е.Краскевич, К.Х.Зеленский, В.И.Гречко . Численные методы в инженерных исследованиях. -- К.: Высш. шк. Главное издательство, 1986.--263 с .