Контрольная работа: Эконометрическое моделирование временных рядов

Задача 1

За год на предприятии были выпущены семь партий продукции, для каждой из которых были определены издержки. Вычислить сумму издержек для следующего плана выпуска.

линейный экономический моделирование

Таблица 1.1.Данные о планируемом выпуске изделий

ед.прод. тыс.шт.	затраты, руб.
2,2	?
3,9	?
5,5	?

Таблица 1.2.Данные о выпущенных партиях

ед.прод.тыс.шт.	затраты, руб.
1	30
2	70
4	150
3	100
5	170
6	215
8	290

Задача относится к разделу Парная регрессия, т.к. в ней даны один независимый параметр (единицы продукции, обозначим как х) и зависимый параметр (затраты, обозначим у).Прежде чем выбирать вид аппроксимирующей зависимости следует представить исходные данные графически.

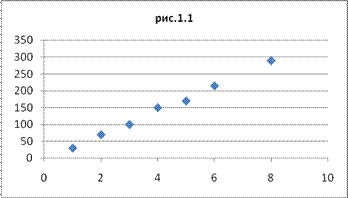
Предполагаем линейную зависимость между х и у

Y=a+bx

Для определения параметров a,b используем метод наименьших квадратов

∑( y –(a+bx))² → min

Функция минимальна, если равны нулю ё, частные производные по параметрам т.е.:

y’a = ∑ (2( y-abx)(-1))=0

y’b = ∑ (2 ( y-a-bx)(-x))=0

или

na+b∑x =∑y,

a ∑x +b ∑x² =∑xy (1)

Система уравнений (1) однозначно определяет параметры a и b – это система двух уравнений с двумя неизвестными. Все остальные величины можно определить из исходных данных :

n- количество исходных точек,

∑x ∑y - суммарные значения параметров х и у по всем точкам,

∑xy - суммарное значение произведения параметров,

∑x²- суммарное значение квадрата величины х.

Рассчитаем коэффициенты линейного уравнения парной регрессии:

Σx^2 = (x^2) - cp –(xcp)^2

b= (cp(y*x) – cp(y)*cp(x))/(σx^2) (2)

a = cp( y) - b*cp(x)

Где индекс cp обозначает среднее значение данной величины, т.е. суммарное значение данной величины надо разделить на n.

Составим таблицу в редакторе Excel.

Таблица 1.3

n	x	y	xy	x^2
1	1	30	30	1
2	2	70	140	4
3	4	150	600	16
4	3	100	300	9
5	5	170	850	25
6	6	215	1290	36
7	8	290	2320	64
итого	29	1025	5530	155
среднее	4,14	146,43	790,00	22,14
σ²	4,98

--> ЧИТАТЬ ПОЛНОСТЬЮ <--