Контрольная работа: Эконометрия
14
февраль
6260
6402.67
15
март
6541
Итого
93019
80152.00
Для определения того, какая из скользящих средних наиболее точно отображает тенденцию, найдем вариацию ряда с учетом полученных средних. Минимум среднеквадратического отклонения осредненных данных и фактических уровней позволяет это сделать по приводимым ниже формулам:
= 608,98, 
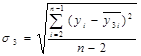= 1002,97, 
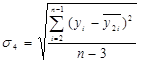= 1478,8
Из расчетов видно, что минимальное отклонение фактических данных от средней обеспечивается при использовании 2-х дневной скользящей средней. Это можно увидеть и при сравнении фактических и средних значений ряда динамики в таблице 1.
Задание:
Сгладить тенденцию ряда (тренд) по одной из аналитических кривых (прямая, степенная, экспонента, гипербола, логарифмическая) по методу наименьших квадратов.
Решение:
Между фактором и признаком, которые находятся в стохастической зависимости существует зависимость, которая называется регрессионной зависимостью. Расчет параметров уравнения регрессии заключается в поиске параметров математического уравнения, наиболее точно описывающего эмпирические значения.
Зависимость результативного показателя от определяющих его факторов можно выразить уравнением парной регрессии. При прямолинейной форме она имеет следующий вид: Yх = а+bх
Если связь между результативным и факторным показателем носит криволинейный характер, то может быть использована степенная, логарифмическая, параболическая, гиперболическая и другие функции.
Наиболее распространенной формой криволинейной зависимости является парабола второго порядка, описываемая уравнением: Yх = а+bх +сх2
Метод наименьших квадратов сводится к тому, чтобы определить параметры уравнения регрессии, путем решения системы уравнений:
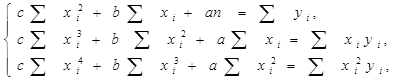
Для определения значений, требуемых для расчета параметров уравнения регрессии по методу МНК рассчитаем исходные значения в таблице 2. Полученные расчетные параметры подставляем в систему уравнений, решаем ее и получаем значения а, b, с для уравнения регрессии.
=> 
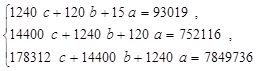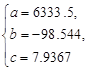
Таким образом, полученное уравнение регрессии имеет вид: y = 7.9367x2 - 98.544x + 6333.5
Таким образом, используя тот или иной тип математического уравнения, можно определить степень зависимости между изучаемыми явлениями, узнать, на сколько единиц в абсолютном изменении изменяется величина результативного показателя с изменением факторного на единицу.
Коэффициент а в уравнении регрессии - постоянная величина результативного показателя, которая не связана с изменением данного фактора. В полученном уравнении регрессии она равна 6333,5 тыс. грн. Параметры b и c показывают среднее изменение результативного показателя с повышением или понижением величины факторного показателя на единицу.
Таблица 2 - Расчетные значения для определения параметров уравнения регрессии
|
Xi |
К-во Просмотров: 434
Бесплатно скачать Контрольная работа: Эконометрия
|