Контрольная работа: Эконометрика 8

2) влияния на зависимую переменную каких-либо других неучтенных факторов.

Статистическая проверка гипотез.

Выдвигаем ноль-гипотезу о том, что коэффициент регрессии статистически незначим:

H ₀ : b = 0.

Статистическая значимость коэффициента регрессии проверяется с помощью t -критерия Стьюдента. Для этого сначала определяем остаточную сумму квадратов

s ² _ост = å ( y_i – ŷ _i )²

s ² _ост = 1,3689.

и ее среднее квадратическое отклонение

s=

s = 0,39.

Затем определим стандартную ошибку коэффициента регрессии по формуле:

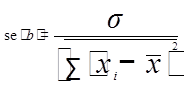
se ( b ) = 0,018.

Фактическое значение t -критерия Стьюдента для коэффициента регрессии:

.

t_b = 427,35.

Значение |t_b |>t_кр (t_кр =2,26 для 95% уровня значимости) позволяет сделать заключение об отличии от нуля (на соответствующем уровне значимости) коэффициента регрессии и, следовательно, о наличии влияния (связи) х и у.

Вывод: фактическое значение t -критерия Стьюдента превышает табличное, значит ноль-гипотеза отклоняется и с вероятностью 95% принимается альтернативная гипотеза о статистической значимости коэффициента регрессии.

Далее построим 95% доверительный интервал для коэффициента регрессии b :

[b – t_кр *se(b ), b + t_кр *se(b )]- 95% доверительный интервал для b.

Доверительный интервал накрывает истинное значение параметра b c заданной вероятностью (в данном случае 95%).

7,6516 < b < 7,7329.

Перейдем к проверке статистической значимости коэффициентов корреляции и детерминации:

r = 0,990;

d = r ² = 0,9801.

Выдвигаем ноль-гипотезу о том, что уравнение регрессии в целом статистически незначимо:

H ₀ : r ² = 0.

Оценка статистической значимости построенной модели регрессии в целом производится с помощью F -критерия Фишера. Фактическое значение F -критерия для уравнения парной регрессии, линейной по параметрам определяется как:

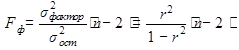
где s² _фактор –дисперсия для теоретических значений ŷ (объясненная вариация);